|
|
|
Caricature and Biography Links |
The Halting Problem of Alan Turing
A Most Merry and Illustrated - well, Illustration
In 1931, Kurt Godel - at the time young unemployed mathematician who lived with his mother in Vienna - published a paper that flummoxed the mathematical and philosophical world. Kurt proved there were unprovable truths. Hailed by some as the first demonstration that a psychological and philosophical principle could be proven with mathematical rigor, Kurt's paper, told us why documents like the Bible and the Constitution of the United States have deep fundamental, but nevertheless, unprovable truths.
Of course, Kurt did nothing of the sort. What he demonstrated was that in formal mathematical systems which are both sufficiently complex and consistent, you can create well-formed formulas - that is, legitimate mathematical expressions - which are true, but nevertheless can't be proven within the system. Since in the same paper Kurt proved very easily that the expression he created was true (by going outside the box, so to speak), it's all the more odd that people said Kurt found there were truths that can't be proven. Today philosophers and mathematicians argue whether Kurt's theorem is of primary importance to mathematics and logic or whether it's overblown. Logicians and philosophers tend to say what Kurt did was as important to the mathematician as Einstein's theory of relativity or Heisenberg's uncertainly principle is to a physicist. But then some advanced mathematicians have said they proceed through their careers with scarce an glance at Kurt's work, thank you. As one mathematics professor recently put it, Kurt warned mathematicians to stay away from certain areas - but those are areas most hard-nosed mathematicians wouldn't go to anyway. Now it's pretty tough for the average reader to access the merits of these discussions. Kurt's paper is pretty hairy. Filled with symbols, theorems, mapping, and definitions (46 of them!), it's kind of ridiculous to expect Joe Blow to set aside the remote on Super Bowl Sunday while Janet Jackson is on the screen and peruse the little Dover paperback, On Formally Undecidable Propositions of Principia Mathematica and Related Systems. We also have a natural and legitimate skepticism when you hear there is a - quote - "proof" - unquote - that relates to the Secrets of the Universe, but, sorry, it's too complex to explain. Fortunately coming up with unsolvable problems became kind of the thing to do in the early to mid-part of the Twentieth Century. Just five years after Kurt published his paper, another of the Twentieth Century's mathematical titans (and oft-cited as the founder of computer science), Alan Turing, came up with a nice little proof for the non-provable. Now known as "The Halting Problem", you actually can set down the remote on Super Bowl sunday and read what Alan has to say. Better yet, you can understand it and not miss a second of Janet. But up front (no pun intended) the reader should be warned. Even when the proof is explained clearly and concisely, many readers have a bit of a "Say what?" reaction. That's due to two things. First, the problem, like many of the more interesting theorems, is an indirect proof. You've probably seen those in school - they're the ones that start off with "Assume that X is true ...". This causes problems for kids trying to prove theorems since they think you can assume what you want is true and then prove it is. Sad to say, this isn't permitted in math. Instead what you do in an indirect proof (also called reductio ad absurdum) is you assume the opposite of what you want to prove. Then you work backwards until you come up with a conclusion that is nonsense, that is, a contradiction. If you do that, we're told, then your first assumption - the opposite of what you wanted to prove - is wrong. So what you wanted to prove in the first place is correct. Actually you shouldn't feel too bad if you feel an indirect proof is, well, indirect. And indeed some mathematicians - called "intuitionists" - don't like using indirect proofs. This is, they don't believe that just because you can prove something isn't true, then you can assume the opposite is. At the same time, strict intuitionists are a minority in the mathematical community, and virtually all mathematicians accept (and use) indirect proofs. Secondly, Alan's proof - and Kurt's - contain a circular reference. This is not the same as a circular argument (which isn't allowed). Instead it's best called self-reference and is where the function uses itself as input. Self-reference is a common feature when proving what's non-provable. Although not - as the rabbi in Fiddler on the Roof said - expressly forbidden, it can leave nagging doubts in your mind that the theorem prover is trying to pull a fast one. For instance, self-references makes perfectly good sense such as "This sentence has five words." Perfectly true even if it refers to itself. But then there's the famous sentence"This statement is not true." If that statement is true, and it refers to itself, then it is not true. And if it is not true, then it must be true. So the statement is both true and false. Now there are various ways around this. And you can argue you have just proven - via an indirect proof - that a statement that refutes its own truth is not actually a statement at all. But it still leaves the question open when can you legitimately use self-reference. For the present, though, this type of stuff is a bit deep of a topic to go into right now (but you might want to check into what Ludwig Wittgenstein wrote about it.) In any case, unlike Kurt's proof, we will find that Alan's is actually quite simple. The main thing is to take it one step at a time and not get ahead of yourself. Alan, as many people know, was concerned with computers (he helped break the secret German codes during World War II). So he framed the problem in computer terms and the problem seems perfectly sensible. Is it possible, he asked, for a computer to tell us automatically whether 1) a solution to a problem exists or 2) if there is no solution? There is a rather quick proof for this. It is an indirect proof which most people encountered in middle school. You make an assumption, derive a contradiction, and so prove your assumption is incorrect. Alan, working in the days before computer had error traps - and in fact, when there were not even real computers - developed an idealized computer. If it would solve a problem, it would stop and give the answer. If it couldn't solve the problem it would keep trying and never stop. Since the goal is to determine if programs will halt or not, it is called the halting problem. So the halting problem asks, can we write a computer program called H, that accepts input of a program P, that will determine if P halts or not? This is show in phony computer language (called pseudo-code by the cognoscenti) as: 
|
|
| If P will halt, then print "P HALTS!" |
| If P will not halt, then output "P DOES NOT HALT!". |
In other words, plug any computer program into HALT and HALT will tell us if the program halts or not. If it does, then we can run the program and get the answer. Or we're immediately told there is no answer and we know not to bother. You could even write a program with HALT as a subroutine where it would check first whether the program would run. eSo clearly HALT then is the ultimate computer program.
The question: Can HALT exist?
The proof is simple and we simply construct a program which we'll called WHOPPER (or W) since it whops HALT.
|
|
| If "H( W )" outputs "W HALTS!", then go into an infinite loop. |
| If "H( W )" outputs "W DOES NOT HALT!", then stop. |
What we see here is that WHOPPER puts itself - that is a copy of its own code - into the subroutines which are our old friend HALT.
So what happens if we try to run WHOPPER? There are only two possible outcomes. Let's consider these separately.
The first possibility is we run WHOPPER and it halts. That means it was the second line that was executed.
But wait a minute! If WHOPPER halts - and is controlled by the second line - that means HALT identified WHOPPER as a program that did not halt! So if WHOPPER halts, that means WHOPPER does not halt!
And if WHOPPER does not halt? Then it means it loops forever and that the control was directed to the first line. But again there's the problem. Control goes there only if HALT says WHOPPER does halt! So if WHOPPER does not halt, that means WHOPPER does halt!
In other words, WHOPPER halts if and only if (as the philosophers say) WHOPPER does not halt. Ladies and gentlemen, we have a contradiction, and our basic assumption HALT exists is false. Therefore there is no effective program that can tell if a program will solve any given problem.
What? Something still bothering you? Something still nagging at the back of your mind?
One thing you see is this program is an example of self-reference. So it is reminiscent of the famous paradoxes that either delight or annoy the reader.
Now self reference isn't - as the rabbi said in Fiddler on the Roof - expressly forbidden. But it is sometimes difficult to understand why one form of self reference is OK ("This sentence has five words") and when it isn't ("This sentence is false"), and you wonder why theorems like Alan's or Kurt's are not paradoxes. The topic is a complex one. Hundreds, if not thousands, of articles have been written about paradoxes and self-reference and there are indications even great mathematicians sometimes aren't so sure. The great Polish mathematician Stanislaw Ulam, who worked with Robert Oppenheimer on the Manhattan Project and Edward Teller on the H-bomb, said he always had the impression that Kurt worried that his own theorem was really nothing more than a new (although crafty and clever) paradox and not a real theorem. But we won't go into that topic right now. Instead we'll show that it is possible to avoid mixing up programs and their input and still prove the Halting Problem. We will do this using the famous diagonal argument of Georg Cantor. If a problem can be solved by a computer, you must write a program it using a finite number of characters. However, the size of the program is open ended and there is really no limit to the number of programs you can write. The same is true for the input. That is both program and input must be limited to a finite number of characters but with no limit to the size. Furthermore you can devise a method to systematically list all possible computer codes and inputs by some method. It can simply be alphabetic (modifked to include the digits 0 to 9 and any supplementary symbols). And once that is done, we can list both the programs and the input in a table where the programs go down the left hand side and the input across the top.
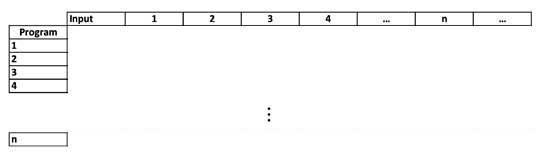
Because we are listing all possible computer programs where each will receive all possible inputs, the table is open ended with no limit to the number of rows and colums. All we require is the number of characters in each program or input to be finite.
Now we can select any two numbers. One will be the program number and the other the input number. So if the halting program exits, we can run it and put the value in the table, and we'll mark that place in the table with an "H" for "Halt". If it keeps looking for an answer we'll let it go on forever. We'll label those places with an "L" for "Loop".
The table then is what we'll call the Universal Turing Machine. The Universal Turing machine allows us - if it exists - to determine whether any program will work or not.T
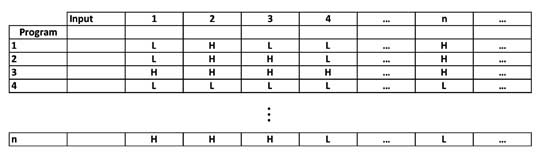
But we ask again can the Universal Turing Machine exist?
Well, if the Universal Turing Machine exists then the table must contain all possible programs to handle all possible inputs. On the other hand, if we can create a new program even if all possible programs have been listed, then we've blown our hypothesis out of the water, and the Universal Turing Machine doesn't exist.
At first glance, it would seem difficult to find a new program with a new sequence of input. After all we've already listed an infinite number of program and input. Besides, how can we tell anyway? We've only listed a small part of the table.
Well, that's where the diagonal argument of Georg Cantor comes in. What we'll do is take the diagonal elements of the table. The diagonal elements are those programs where the program number just happens to be the same as the input number. These are the elements marked in red below.
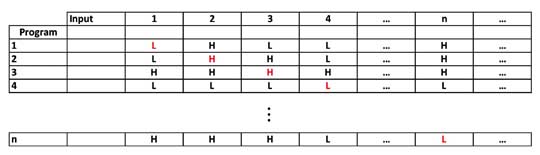
Next we switch every "H" on the diagonal to a "L" and every "L" to an "H". Then we write them in a row and say that is the output of Program D.
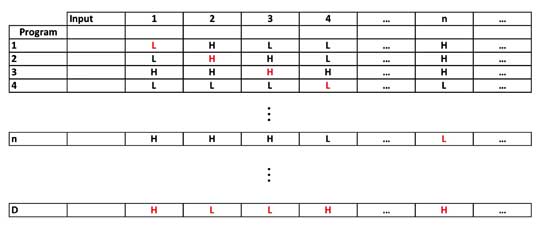
All right. If our hypothesis is true - that our original table has all the possible Turing Machines and their output - this new list must also be somewhere in our original table.
Well, which program can Program D be? It can't be Program #1 because that machine has "L" as the output for Input #1 Program 1 has "H" for that input. It can't be the second machine because that has "H" as the output for the second input and our new row has "L". In fact, if you go down to any row, you'll find the program can't be anywhere in our original list. Wherever we had a "H", we now have a "L" and vice versa. That means we've just created a new program out of all possible programs. That's impossible and so our fundamental hypothesis must be incorrect. Ergo, the Universal Turing Machine does not exist.
Now tables are not usually considered bona fide proofs. So we really should cast the tabular demonstration into a more acceptable form. We also don't want to mix up the programs with the inputs. So let's create a new program with number n as follows:
|
|
| If H(n, n) writes "H", then LOOP; |
| If H(n, n) write "L" then HALT; |
Note that our new program is defined from a program that is already completely specified. So you don't have to define it before you define it. And the program does not use itself. So our concerns happily vanish into thin air.
But if our Turing machine covers all possible programs P(n, x) must be in the list. Where is it, then. That is, what number is n?
Well, here we go again. Pick any number n. It can't be 1 because if Program 1 with Input 1 loops, then Our Program with Input 1 halts. If Program 1 with Input 1 halts, then Our Program with Input 1 loops. Cain't be Program 2 either because if you use Input 2 you see the same thing. So once more we conclude our hypotheses - H(x, y) and the Universal Turing Machine exist - is false.
At this point, some people may ask if we can salvage our program by simply making room for the new program. That is using it as another axiom. Then the Universal Turing Machine would contain the program we created. So we advance each row by one and slip in P(n, x) at the first. So P(n, n) become Program 1 and the Older Program 1 becomes New Program 2. So our new program is now part of the list, right?
Soddy, old chap, but we can now do exactly the same thing again. We can simply define a program Q(n, x) identical to P(n, x) but using the new list. Then Q(n, x) can't be the new list for the same reason P(n, x) wasn't in the old list. So no matter how many new functions we add, we can always create one that isn't. So the conclusion is still the same. There is no effective solution to determine if any problem can be solved or not.
At this point, some readers may wonder if we're really asking the right question. Regardless of the technical correctness of the proof, just how important is the Halting Problem to the real world? After all, we have defined a program P(n, x) to confuse another program. Does that lack really help computer scientists in their day-to-day jobs? What good is that?
And remember Kurt. He proved a theorem that in effect says it can't be proven. But does that really hinder mathematicians who have to do real work?
In fact, CooperToons has found some mathematicians who are, in fact, quite bored by theorem's like Kurt's and Alan's). On occasion he's asked Ph. D. mathematicians to clarify points in Godel's work. The responses range from a rolling of the eyes as in "Oy, vey! Not Godel again!" to "Dunno. Go ask a logician".
But what Kurt and Alan did was throw up a warning sign for mathematicians and computer scientists. They proved there were areas you should not waste your time with. For instance in the later nineteenth and early twentieth century, there were mathematicians like David Hilbert and his friends were trying to prove all properly constructed formulas could be proven or disproven. Kurt and Alan showed this was not the case and David should look for something else to prove..
Finally we need to point out that neither Alan nor Kurt said there are unsolvable problems. And undecidable formulas have been around for years. You don't have to cite Paul Cohen's proof that the Continuum Hypothesis was undecidable. Shoot, we can go back to Euclid and his famous Fifth Postulate. After thousands of years of people trying to prove it, it was finally shown =that it's truth or falsity depends on your system and that there are some systems where it's true and others that it's not. Decide on your system and you can prove which answer is correct. And Mojzesz Presburger was able to design a system of numbers, commensensically called Mojzesz arithmetic, that is a complete system and has no undecidable formulas. Best of all, you don't have to learn multiplication tables.
Some people take delight in Kurt's and Alan's theorems and say that these theorems prove man's intellect is something more than a machine. But you have to wonder. After all when computers began to arise in the world and even after the onset of the computer revolution of the 1980's, it was still said that computers would never be able to beat chess grandmasters. After all, we were told computers could not develop overall strategy that a human brain could. But we now have computers that do beat grandmasters and before long (CooperToons hypothesizes) we will have computers that can always beat any grandmaster at chess. After all, we now have computers that beat humans at Jeopardy!
So maybe the best question should actually be "Are humans just complex but imperfect and slow computers?"
Perhaps we should compute on this a little.
References
Alan Turing: The Enigma, Andrew Hodges, Simon and Schuster (1984). Alan's volumous biography.
"Alan Turing", The MacTudor History of Mathematics Archive, http://www-history.mcs.st-andrews.ac.uk/Biographies/Turing.html. Probably one of the best sources for biographies of mathematicians and logicians on the web. Huge number of entries from ancient to modern times. Most entries have a lot of detail about the people. And thank heavens it's a non-commerical website. No animation, no ads, and easily navigated. The home page is: http://www-history.mcs.st-andrews.ac.uk/
"On Computable Numbers with Applications to the Entscheidung-Problem", Proceedings of the London Mathematical. Society, Vol. 42, 230-265 (1936). Alan's paper doesn't use modern programming and shows that a "Turing Machine" can be given a problem it can't solve. Still, it's worth the effort to understand Alan's original argument and methodology.
Online at http://www.turingarchive.org/browse.php/B/12 but not in a terribly convenient form.
"Computing Machinery and Intelligence", Mind Volume 59, pp. 433-460. Alan's original paper on the imitation game ("The Turing Test"). Easy to read and understand. An online vesion is at http://www.loebner.net/Prizef/TuringArticle.html
"Alan Turing", http://plato.stanford.edu/entries/turing/ The Stanford History of Philosophy - Online, free, no registration, but not (thank goodness) completely open to all writers - you have to be an expert to write for SHP. This article is by Alan's biographer, Andrew Hodges
"Does Gödel Matter? The romantic's favorite mathematician didn't prove what you think he did.", Jordan Ellenberg, http://www.slate.com/id/2114561/. Jordan is professor of mathematics at the University of Wisconsin and points out that most mathematicians work with equations like "2 + 2 = 4" rather than (x)~Bew(x) which is what Kurt did. Under most definitions of the concept "number", then "2 + 2 = 4" is always true and you can prove it. So Kurt proved there are equations which don't do anything other than say they can't be proven? Many mathematicians simply say "Who cares?" and get back to work.
"Official Alan Turing Website", http://www.turing.org.uk/turing/index.html The web site is also by Andrew. Quite a lot of information. One gripe: flickering, if minor, animation
Return to Alan Turing Caricature