Cantor's Diagonal Argument
A Most Merry and Illustrated Explanation
(With a Merry Theorem of Proof Theory Thrown In)
(And Fair Treatment to the Intuitionists)
(For a briefer and more concise version of this essay, click here.)

George showed it wouldn't fit in.
A Brief Introduction
Not too long ago while surfing the TV channels, you could lean back, press the remote, and suddenly you found a show about Georg Cantor (pronounced "GAY-org", but we'll call him "George"). The story told of how George, one of the most important mathematicians in history, went insane while grappling with the concept of infinity.
Although not really a bad introduction to the work of George (and the accomplishments of three more mathematicians and physicists) it's highly questionable that his work was the primary cause of his mental health problems. And because the show was intended for a general audience, it did not go into details of what George actually did.
On the other hand the only way to appreciate the profundity of George's work is to see exactly what he did. True, many of the mathematical discoveries during and after the 19th century are difficult to understand. But what George discovered was undeniably one of the slickest mathematical tricks ever, and it's easy enough to follow for anyone who has reached middle school mathematics.
Counting the Infinite
George's most famous discovery - one of many by the way - was the diagonal argument. Although George used it mostly to talk about infinity, it's proven useful for a lot of other things as well, including the famous undecidability theorems of Kurt Gödel.
George's interest was not infinity per se. What he was doing was developing set theory.
Pretty much everyone accepts that some sets are infinite. The sets of counting numbers, integers, and the points on a line are all infinite.
But the concept of infinity was not well defined. Just saying an infinite set is unlimited is simply saying an infinite set is infinite. So George decided he needed to come up with a precise mathematical definition.
George started things off simply. He just considered the counting numbers.
N = { 1 , 2 , 3 , 4 , ..... }
George realized that the counting numbers had no upper limit. Otherwise you could add 1 to the biggest number and not get a higher number. But that was absurd. If you add 1 to any number, you'll always have a higher number1.
Footnote
Some may think what we've said is just a disguised circular argument. That is, we know there isn't a highest number because we can always add 1 to a counting number and get a new number. But then we said we know we can always get a new number by adding 1 because there is no highest number!
But look at it this way. If there is a highest number, NHighest, then adding 1 to it means it must be less than or equal to itself.
| nHighest + 1 | ≤ | nHighest |
Well, then we can - as an American president said - reason together.
| nHighest + 1 | ≤ | nHighest |
| 1 | ≤ | nHighest - nHighest |
| 1 | ≤ | 0 |
So if there is a a highest counting number, then:
1 ≤ 0
... which is complete nonsense.
The only conclusion then is:
THERE IS NO HIGHEST NUMBER!
This property - that every counting number has an immediate successor - is how George defined the infinity of the counting numbers. He named this infinity a countable infinity.
George, though, also stumbled on some oddball properties of countably infinite sets. For one thing sometimes only a small portion of a countably infinite set is also countably infinite.
Now most people would say there are only half as many even numbers as counting numbers. But George showed you can put both the counting numbers and the even numbers into a one-to-one correspondence2.
Footnote
This type of one-to-one correspondence was noticed by none other than Galileo in 1638 but even in a stranger way. Galileo pointed out that each number could be paired off with its square:
| 1 | → | 2 |
| 2 | → | 4 |
| 3 | → | 9 |
| 4 | → | 16 |
| 4 | → | 25 |
| ⋮ | ||
| n | → | n2 |
| ⋮ |
What Galileo thought was odd was that as n increases, the squares, n2, are separated by more and more numbers - that is, they become sparse. But the size of the two sets is the same.
| 1 | → | 2 |
| 2 | → | 4 |
| 3 | → | 6 |
| ⋮ |
This is an odd finding because putting elements of a set into a one-to-one correspondence is how we count the members of any set. If you pair the elements of a set with as many sequential counting numbers as possible, then the highest counting number of the pairings is the set's size.
So we see that for the set { 1 , 89 , 1234 }, the size is 3.
| 1 | → | 1 |
| 2 | → | 89 |
| 3 | → | 1234 |
But you don't have to actually count the elements to determine if two sets are the same size. All they need to do is pair up. For two sets { 1 , 89 , 1234 } and { ½ , ⅔ , ¾ }
| 1 | → | ½ |
| 89 | → | ⅔ |
| 1234 | → | ¾ |
... we see they are both the same size.
And so the counting numbers and even numbers - infinite sets though they are - with their one-to-one correspondence:
| 1 | → | 2 |
| 2 | → | 4 |
| 3 | → | 6 |
| 4 | → | 8 |
| 5 | → | 10 |
| ⋮ | ||
| n | → | 2n |
| ⋮ |
... must also be the same size.
This is a weird property. We have a set - the counting numbers - which is the same size as one of its own proper subsets, the even numbers3. In finite sets, a proper subset is always smaller than the original set.
Footnote
A set A has a subset, B, if every element of B is also an element of A. Since by this definition, every set is a subset of itself, we also define a proper subset.
A set A has a proper subset B if every element of B is also an element of A but every element of A is not an element of B.
So for the set { 1 , 89 , 1234 }, both:
{ 1 , 89 , 1234 }
... and ...
{ 89 , 1234 }
... are subsets. But:
{ 89 , 1234 }
... is a proper subset.
The other proper subsets for { 1 , 89 , 1234 } are { 1 }, { 89 }, { 1234 }, { 1 , 89 }, { 1 , 1234 }, and the empty set { } (also represented as ∅.
Another weird property is that if you combine a countably infinite set with another countably infinite set, the new set is also countably infinite. So both sets are the same size.
We see this if we consider the set of integers.
The set of integers is simply the counting numbers (ergo, 1, 2, 3, etc.) grouped with their negatives (-1, -2, -3, ...) and zero. You'd think there would be more integers than counting numbers.
But you can prove the number of integers is the same as the counting numbers simply by setting up the following one-to-one correspondence.
| 1 | → | 0 |
| 2 | → | -1 |
| 3 | → | 1 |
| 4 | → | -2 |
| 5 | → | 2 |
| 6 | → | -3 |
| 7 | → | 3 |
| ⋮ |
You can write this correspondence as an actual formula:
f(n) = (-1)(n+1)n/2 - [(1 - (-1)(n)])/4
... where if you plot each counting number, n, against f(n) you get the one-to-one correspondence of the counting numbers to the integers we show above.
Try this formula. Like the commercials say, it really, really works.
And finally - although it's a little more complex and strange - George showed that the fractions - the rational numbers - are also countably infinite4.
Footnote
At this point, we have to admit that although we have shown the formulas for the one to one correspondence of counting numbers and the other sets, we have not actually proven the formulas are correct. This would require a process called mathematical induction. It can be a bit tricky but not so tricky that the average person can't understand it. For a Most Merry and Illustrated Essay with an introduction to induction click here.
Things were certainly getting very strange.
George Figures It Out
What stamped George as a great mathematician is he didn't worry about the strange results (although some of his colleagues did). Since the weird conclusions came from proper reasoning, he just accepted them.
But some things had to be clarified. George realized that saying countable infinite sets were the same size was not precise. Instead of talking about the size of a set, George spoke about a set's cardinality.
There was, though, no actual number for the "cardinality" of a countably infinite set. The usual symbol for infinity, ∞, was too vague. So George decided to borrow the Hebrew letter aleph, ℵ, and he called the countable infinity cardinality, ℵ0, or aleph-null.
Why did George add the zero subscript? Well, he began to think that a countable infinity was the tip of an infinite iceberg. And that's when he came up with the diagonal argument.
The PROOF
George's diagonal proof, we should mention, is an indirect proof. That is, you:
 |
Assume the opposite of what you want to prove. |
 |
Start to reason until you come to a statement we know is FALSE. |
 |
Then we know (so the logicians tell us) the opposite of what we tried to prove is incorrect. |
 |
So what we wanted to prove in the first place is true, after all!5 |
Footnote
The proof that indirect proofs are valid is quite simple using symbolic logic.
Suppose you're trying to prove a statement S. Then you first assume ¬S.
Next you assume that ¬S implies a CONTRADICTION, A ∧ ¬-A.
This is written symbolically as:
¬S → A ∧ ¬A
Using the rules of symbolic logic we find:
¬S → A ∧ ¬A
¬(¬S) ∨ (A ∧ ¬A)
¬¬S ∨ (A ∧ ¬A)
S ∨ (A ∧ ¬A)
Since a contradiction, A ∧ ¬A, is always FALSE, we now have:
S ∨ FALSE
Since TRUTH of:
¬S → A ∧ ¬A
... is assumed to be TRUE, then:
S ∨ FALSE
... is likewise TRUE.
So that S is TRUE follows immediately.
We'll see that this is what George did. And in doing so he invented the diagonal argument.
The diagonal argument starts off by representing the real numbers as we did in school. You write down a decimal point and then put an infinite string of numbers afterwards. So you can represent integers, fractions (repeating and non-repeating), and irrational numbers by the same notation.
| Type of Number | Representation |
| Integer | 1.0000000000000000000000000.......... |
| Non-repeating fraction | 0.2500000000000000000000000.......... |
| Repeating fraction | 0.1231231231231231231231231.......... |
| Irrational Number | 1.4142135623730950488016887......... |
Remember George was using an indirect proof, and he wanted to prove you could not put the real numbers into one-to-one correspondence with all the counting numbers. So he assumed you could.
To make things simpler, though, he restricted the real numbers to those between 0 and 1. If those numbers can't be put into a one-to-one correspondence with counting numbers, then the rest of the points on an infinite line sure can't either.
A partial list of the one-to-one correspondence might look something like the following table. Again this isn't to be taken too literally but is simply a hypothetical example.
|
(Hypothetical) Place in List |
Number |
| 10 | 0.00000000000000000000000.......... |
| 128931 | 0.50000000000000000000000.......... |
| 583910 | 0.41421356237309504880168.......... |
| 3291293 | 0.51515151515151515151515......... |
| 78481839 | 0.71828182845904523536028.......... |
| 948118319 | 0.14159265358979323846264.......... |
But partial hypothetical lists won't help us prove the theorem. What we need is a more general representation, all the better to reason with.
So what we do is dream up a symbolic list. Ergo:
| Place in List | Number |
| 1 | 0.d11d12d13d14d15d16d17d18d19 .... |
| 2 | 0.d21d22d23d24d25d26d27d28d29 .... |
| 3 | 0.d31d32d33d34d35d36d37d38d39 .... |
| 4 | 0.d41d42d43d44d45d46d47d48d49 .... |
| 5 | 0.d51d52d53d54d55d56d57d58d59 .... |
| ⋮ | |
| n | 0.dn1dn2dn3dn4dn5dn6dn7dn8dn9 .... |
| ⋮ |
Now if it is true there is the one-to-one correspondence with the counting and real numbers, then it will be impossible to find another real number that's not in our list.
But what happens if we do find another real number? Well, then we've found our contradiction.
And if we find a contradiction, that means our initial assumption - that there is the one-to-one correspondence of counting and real numbers - can't be true.
And that would mean that the infinity of the real numbers is not the same infinity as the counting numbers. That is the two sets do NOT have the same cardinality.
In fact, it turns out our mysterious new number is very easy to write. Call it m and define it as:
m = 0.(d11+1)(d22+1)(d33+1)(d44+1)(d55+1)(d66+1).....(dnn+1)....
In other words. take the diagonal elements of the original list - that is, take d11, d22, d33, d44, d55 and all the rest - and then add one to them. Then line them up after a zero and a decimal point.
This is a real number. And if our assumption that the real numbers and counting numbers have a one-to-one correspondence it true, then m must be somewhere in our original list.
(Strictly speaking, what we do is slightly more complicated. If dmm is 0 through 8, then we substitute dmm + 1 for dmm. But if dmm = 9, the dmm becomes 0).
Does It Fit?
All right. Just where does our number m fit in the list?
Well, it can't be the first place because the first number after the decimal point is d11, and m has (d11+1).
It can't be the second place either since the second number is d22. And m has (d22+1).
Third place? Nope. That has d33; m has (d33+1).
It's the same for any number you pick. There is no place in the whole list where you can put the new number, m. Therefore for any counting number n the new number cannot be put in the list since the original list had dnn and our new number always has (dnn+1).
We have the contradiction of the indirect proof.
And the consequence?
 |
The counting numbers canNOT be put into a one-to-one correspondence with the real numbers. |
... which also means:
 |
The counting numbers and the real numbers do NOT have the same cardinality. |
At this point it's tempting to say, "Well, you can add one element to a countably infinite set and still have a countably infinite set. So we'll advance every number by one place, and stick in the new number. So now we have our one to one correspondence with the counting numbers.
Well, that doesn't work either. You can still take the new diagonal, add one to each number, and come up with a number that's not in our new list. You can't win, and the real numbers and counting numbers cannot be put in a one-to-one correspondence.
The lack of the one-to-one correspondence of the real numbers and counting numbers means there's too many real numbers to count. Now that means we have two types of infinity. One is countable (for the counting numbers) and the other infinity (for the real numbers) is uncountable.
Calling a spade a spade, George called this new and uncountable infinity an uncountable infinity. And it turns out a lot of sets are uncountable: the real numbers, the number of points on a line, the number of points on a plane; stuff like that.
Since our uncountable infinity is larger than the earlier infinity, ℵ0, George called its cardinality, aleph one, ℵ1.
How are the two infinities related? As we'll show below George decided there was a formula:
ℵ1 = 2ℵ0
This equation formed the basis of what George called the continuum hypothesis. The continuum hypothesis posited that there were no infinities between ℵ0 and ℵ1. That is, there is no set whose cardinality is between that of the counting numbers and the real numbers.

Kurt and Paul
They finally solved it.
Despite George's efforts to prove the continuum hypothesis, he had no luck in doing so. That's because it can't be proven. That was shown by two 20th century mathematicians. In 1940, Kurt Godel showed the continuum hypothesis cannot be disproven with the set theory axioms. Then in 1963 Paul Cohen proved it can't be proven either.
That means the continuum hypothesis is like Euclid's fifth proposition. It is independent of the other axioms of set theory. If you want, you can create a set theory where the continuum hypothesis is true. Or you can create a set theory where it is not.
Objection! Objection!
The diagonal argument bothers a lot of people, and you will find much brouhaha on the Fount of All Knowledge (i. e., the Internet) that attempts to prove it is wrong. The objections, though, can be distilled down to simple and subtle misunderstandings.
As we mentioned before, the most common objection is that you should be able to bump-up-the-numbers and slip in the new diagonal number. So you still have a countable infinity.
But George's Friends point out this is a never ending goose chase. When you bump up a number to slip a new one in, with the diagonal method you can then create new number that's not in the list. So bumping up numbers doesn't help.
Of course, the George Objectors say, well, just bump the numbers up again. Then you can slip in a new number and again get your one-to-one correspondence.
And it goes on and on.
Which argument is right? Does the never ending goose chase mean you can slip a new number in? Or doesn't it?
Actually the goose-chase/number-bumping argument is irrelevant. Instead, to prove George wrong, the George Objectors have to show that once you make a one-to-one correspondence of the real and counting numbers, you can never create a new number that's not in the list.
But the diagonal argument shows that you can. So George was right and there's nothing we can do about it.
At this point we'll say there are mathematicians - quite legitimate ones - that don't accept George's proof. That's because in creating his proof he just waved his hands and said "Let there be a one-to-one correspondence". He did not show us how to construct the correspondence between counting numbers and a unique real number. Until he does that, they say, George's theorem is at best incomplete.
Fortunately, in the next section we will see how to devise an effective method that does indeed construct unique real numbers and assigning them to every counting number. Then we'll create a new number that can never be in the list - no matter how much you bump up6.
Footnote
Another objection you'll find on the Fount of All Knowledge is the use of three dots - like "..." - to indicate a continuing sequence of numbers. The claim is that this proves you can't really have infinite sets since there's no way to represent them.
The three dots, though, is simply a way to simplify more rigorous notations. And the greater rigor is what we have below.
George could have pulled it out of his - ah - hat.
George the Effective
The first step of the diagonal proof, we will restate, is assuming you can pair the real and counting numbers. But George's critics say we did not construct a unique pairing. A real theorem must do this.
All right. We'll add some rigor here and point out that our pairing is actually a function. This function maps the counting numbers to a unique real numbers.
To middle school students a function is a formula that you have to plot on a graph. But more generally and rigorously, a function is an ordered pair of numbers. In our case, the first number of the pair is a counting number and the second number is a unique real number. Our function is the set of all such ordered pairs.
More exactly we define our function as:
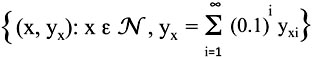
A bit of explanation is clearly in order. What the formula above means is we have defined a set of ordered pairs (x, yx) where x is a member of the counting numbers (the script N stands for the alternative name of the counting numbers, the natural numbers). This means that there are as many ordered pairs as counting numbers.
The second element of the ordered pair yx is defined as:
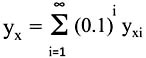
The part of this equation, yxi, is in turn defined as:
yxi = RND( {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} )
That is, yxi is simply a single digit from 0 to 9 but randomly selected.
Knowing that the capital letter Sigma, Σ, represents summation, we see that yx is a number represented by a decimal point followed by a random infinite series of the digits from 0 to 9. Ergo, the ordered pair (x, yx) has a counting number for the first number and a real number for the second.
First we need to deal with the pesky requirement that yx values are unique. But fortunately we don't need to have some algorithm to weed out the repeats since there can be no repeats. A little reflection tells us that no two values of yxi are identical.
Alas, for those for whom the reflection does not yield immediate gratification, consider two numbers. Call them, yr and ys. We will define them as we did yx but sum over a finite number, k, of randomly chosen digits.
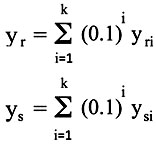
For instance, if k = 10, then yr and ys could be.
yr = 0.4408754017
ys = 0.8598501984
Now of course if we kept trying we would eventually end up with two values that happen to be equal.
yr = 0.5200845709
ys = 0.5200845709
But just what is that probability of this happening? That is, how often will yr and ys will be the same?
Well, that's easy enough to calculate. Since we have k digits (here k = 10), the probability that two series of digits of length k are equal is given by:
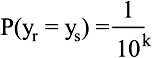
That is, if, we have two series of numbers that are 2 digits long, the odds that the numbers are equal is 0.01. If they have three digits, then the odds are 0.001 they will be the same. With 10 digits (as we have in our example) we have a probability 0.0000000001.
So if yr and ys have an infinite number of digits:
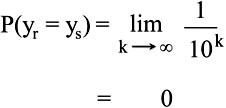
This means that with our definition of yx as an infinite number of random digits after the decimal point, no two yx values can ever be the same. Ergo, each yx will be unique.
(Note: We emphasize that if k is a finite number, there is some probability that two numbers will not be unique. Then if you create enough yx values, eventually you'll find two that are the same. This is the famous Birthday Problem but generalized.)
What we have done here is not just make a hypothetical "assume there is a one-to-one correspondence, etc. etc." generalization. Instead, we have defined an effective method for generating unique real numbers, each of which can be assigned to a unique counting number.
Although you can't write out the entire real number - it's infinitely long after all - you can find what any digit is at any location in the real number. Pick the digit and generate a random number. That's your digit for that number at that location.
But ... but, George's critics say. You don't know what the random number is until you generate it after you've already generated it! So when you find out what the number is, it won't be the same number.
Well, not really. You can, if you wish, look at the issue in a modernistic manner in which the instance does not occur without the observation. Sort of the mathematical analog of Schrödinger's Cat.
In any case it doesn't matter. The properties derived from a sufficiently large collection of random numbers will be the same regardless of the individual values. That is, if you have generated enough random numbers for obtaining a general characteristic of the ensemble, then replacing the original random numbers randomly will not change the property therein determined (using big words here). Ergo, you're gonna get the same answer no matter when you take a peek.
George's Critics still object. They say that using limits as we did does not mean that any individual number will have the property of the limit - i. e., that the two numbers in the list will not be the same. Instead for any number, k, no matter how high, there is always a finite probability two numbers will be equal.
Naturally George's friends laugh behind their hands. The critics, they say, are only referring to sets with finite values of k - not to a true infinite set. So George was right.
A Gentlemen's Disagreement
(Or When Is Infinity Not Infinite?)
The last objection and rebuttal reveals the fundamental disagreement with George and his critics. The critics do not accept that infinite sets exist as a totality. Infinity, they say, is something that can never be reached. There is no actual infinity only a potential infinity. So a property of a set defined in terms of a limit is not a property of the set itself.
George and Hs Friends, though, say actual infinite sets do exist. So some properties of an infinite set do indeed take on the properties of the limits - properties which are not shared any finite subset, no matter how large.
With these objections now tidied away - although most of George's critics aren't convinced - we now return to the diagonal argument itself.
The Diagonal Argument (Again)
So far we've shown you can actually construct an infinite number of unique real numbers paired off with the counting numbers. And as before if there are the same number of real numbers as counting numbers, then there cannot be any more real numbers than the ones we have constructed.
But if we can construct at least one more real number that's not in the list, then the two sets do not have the same cardinality. Therefore there are more real numbers than counting numbers.
By now you know how we do that. Yes, we'll just take our previously defined ordered pairs, (x, yx) and keeping in mind that yx is built up from a series of digits, yik, we'll write the following ordered pair:
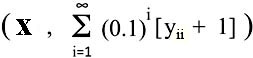
Here yii is digit i from number yi of our previously defined set of ordered pairs. As before if yii = 9, then we take yii + 1 = 0, not 10.
(Note: For you sticklers for exactness, that means we actually define the ordered pair, as { x, Σmod( [yii + 1] / 10) } )
All right. Can the ordered pair 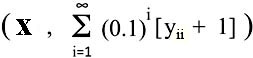 be in our original set? Or rather what value of x can we select so
be in our original set? Or rather what value of x can we select so 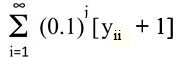 is equal to some yx of our original ordered pairs?
is equal to some yx of our original ordered pairs?
Since no value of a counting number i is equal to i + 1, there is no such x. Furthermore, no matter how we change the real numbers - such as by substituting new random digits for the old ones - that doesn't help. The number defined as 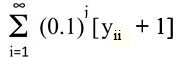 will always be an extra number not in the original list. So you will always have more real numbers than counting numbers.
will always be an extra number not in the original list. So you will always have more real numbers than counting numbers.
Objection! (Again?)
Despite the proper and logical validity of the diagonal argument, it just seems too much for some people to accept. Part of the problem is that it is, after all, an indirect proof which to some seems sneaky.
We have mentioned that there is a group of legitimate mathematicians and philosophers who have taken exception to George's conclusions about infinity. These Objectors to George are called Intuitionists of whom the mathematician Luitzen Egbertus Jan Brouwer was the leader.
Bertus (as Luitzen was called) and his friends did not question the validity of George's theorems given his assumptions. Instead, they questioned the underlying assumptions themselves. Their biggest gripe is that George and his friends accept the Law of Excluded Middle.
The Law of Excluded Middle means either a statement or its negation is TRUE.
That is, for any statement A:
A or not-A
... is always TRUE.
Although the truth of the statement A or not-A seems obvious, it is surprisingly important in mathematics. It is, in fact, absolute necessary if indirect proofs are to work.
Suppose, for instance, that you can't prove A directly. But somehow you have proven that not-A is impossible. By the Law of Excluded Middle you have nevertheless proven A. This is exactly how an indirect proof works.
Virtually all proofs regarding infinite sets are indirect proofs. You almost never see a deductive proof where you start with established statements and end up with a new conclusion. Instead as we've said before, you prove what you want by assuming it's false and then arrive at a statement that can't be true. This proves that your original statement - which your proof assumed to be false - is true after all.
But the Intuitionists say that the Law of Excluded Middle was derived from simple finite systems by old-timey guys like Aristotle. Over the years it's been forgotten how limited it's application really is. There is, the Intuitionists say, no reason to accept that it applies in all cases and certainly you shouldn't accept it unquestionably when dealing with infinite sets.
For instance, another of George's important theorems was to prove that the number of subsets of the counting numbers was uncountably infinite and equal to the real numbers. He did this by, yes, an indirect proof using a version of the diagonal argument.
For finite sets, if a set has n members, there are 2n subsets. You can collect these subsets into its own set called the power set. So the cardinality of the power set of a set with n members is 2n.
George concluded that this relation of cardinality of a set to its power set applied to countably infinite sets as well. So if the number of members in a countably infinite set - its cardinality - is ℵ0, then cardinality of its power set is the equation we saw above:
ℵ1 = 2ℵ0
It was ℵ1 that George concluded was the cardinality of the real numbers.
But what about the power set of real numbers? That is, the power set of the power set of the counting numbers. Using the same reasoning as before George called the cardinality of this set ℵ2 and it's calculated by:
ℵ2 = 2ℵ1 = 2ℵ02ℵ0
You can see where we're headed. You can keep going forever and have ℵ3, ℵ4, ℵ5, ℵ6 ... and on up.
These numbers - and they really are numbers - are designated by ℵi and are called transinfinite numbers. There's a never ending supply of them and they have their own properties and - yes, books have been written about them and fancy pants courses are offered about them at universities.
And all from George's diagonal argument.
Objection! (Ad Infinitum)
But there's still those pesky Intuitionists! They still don't accept indirect proofs for infinite sets.
Instead they say you must limit all proofs - even of infinite sets - to constructive proofs without the Law of Excluded Middle. With these restrictions, they point out, George's Wonderful House of Infinities comes a-tumbling down.
Well, you say, we'd really like to see how that is possible.
I thought you would as Captain Mephisto said to Sidney Brand. It's very simple really.
First we'll look at George's claim that the power set of the counting numbers is uncountable. We'll do this by starting small and moving on to larger set sizes.
Take the set of counting numbers in sequence from 1 to any value n. For n = 3, the set is:
{ 1 , 2 , 3 }
... and so the power set is:
2{ 1 , 2 , 3 } = { { 1 } , { 2 }, { 3 }, { 1 , 2 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 }, ∅ }
Notice that the first three subsets:
{ 1 } , { 2 } , { 3 }
... can be put in a one-to-one correspondence with the counting numbers up to the highest elements in the set:
| 1 | → | { 1 } |
| 2 | → | { 2 } |
| 3 | → | { 3 } |
This in turn means that there are elements that are left over and canNOT be put into one-to-one correspondence with the elements in the set:
{ 1 , 2 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } , ∅
... where ∅ is the empty set - { } - which is always a subset of any set7.
Footnote
Some people scratch their heads that something with nothing can be part of something that has something. But look at it this way.
A set A is a subset of set B if every element of A is an element of B. So if A is not a subset of B then there must exist at least one element of A that is not an element of B.
But if A has no elements, then it is impossible for it to have an element that's not in B. The only conclusion is that if A has no elements it is an subset of any set.
Yes, this is an indirect proof. The direct proof is best shown in symbolic logic.
If a set A is a subset of B
A ⊆ B
... then the following statement is true:
∀x: x ∈ A → x ∈ B
... which means "For all x, if x is an element of A then x is an element of B."
But if A is the empty set:
A = ∅
... we know ...
x ∈ A
... is always FALSE.
But in first order logic an IF-THEN statement:
X → Y
... is always TRUE if X is FALSE.
So ...
x ∈ ∅ → x ∈ B
... is always TRUE.
It immediately follows that:
∅ ⊆ B
The empty set is an element of any set.
We can generalize our findings. For any set whose elements are 1 and the sequential counting numbers up to n, the elements of the set can be put into a one-to-one correspondence of the subsets with only a single element:
{ 1, { 1 } }
... to ...
{ n , { n } }
So after we do our one-to-one correspondence with the single element subsets, there are a total of 2n - n subsets that are left over. And for all practical purposes, the number of these leftover subsets increases exponentially as n goes up.
Because the extra subsets increase exponentially with n, there will always be an infinite number of subets that cannot be counted - and the number of subsets of our countable infinity is in fact a non-countable infinity.
Just like George reasoned using his indirect diagonal proof.
Hold on there! say the Intuitionists. You stopped too soon. Let's actually look at the number of excess subsets.
If there are 2n subsets of the number from 1 to n, and you match each single number subset { n } with the number n, the number of leftover subsets 2n - n is large, but finite. Therefore the set of these excess sets for any value n is countable from 1 to 2n - n.
Again we'll illustrate what we're talking about using n = 3. Clearly n and the single member subsets { n } sets can be put into a one-to-one correspondence:
| 1 | → | { 1 } |
| 2 | → | { 2 } |
| 3 | → | { 3 } |
The 23 - 3 left-over sets can also be denumerated with counting numbers:
| 1 | → | ∅ (The Empty Set) |
| 2 | → | { 1 , 2 } |
| 3 | → | { 1 , 3 } |
| 4 | → | { 2 , 3 } |
| 5 | → | { 1 , 2 , 3 } |
The union of these groups of sets is, of course, the power set. But the members of the power set can still be put into one-to-one correspondence with a finite set of counting numbers:
| 1 | → | { 1 } |
| 2 | → | { 2 } |
| 3 | → | { 3 } |
| 4 | → | ∅ |
| 5 | → | { 1 , 2 } |
| 6 | → | { 1 , 3 } |
| 7 | → | { 2 , 3 } |
| 8 | → | { 1 , 2 , 3 } |
Or in general terms:
| 1 | → | { 1 } |
| 2 | → | { 2 } |
| 3 | → | { 3 } |
| ⋮ | ||
| n + 1 | → | ∅ |
| ⋮ | ||
| 2n | → | { 1 , 2 , 3 , ... , n } |
We conclude, then, - and pardon if the Intuitionists shout:
FOR ANY SET of numbers from 1 to n, NO MATTER HOW LARGE, THE POWER SET IS DENUMERABLE FROM 1 TO 2n.
So George is indeed full of bullshine, horse hockey, and poppycock.
Huh! snort George's friends. Not, as Eliza Doolittle said, bloody likely. All you've done is prove that the number of subsets of a finite set is equal to 2n.
But more importantly you have proven that the power set of any set always has a higher cardinality than the set itself. And so the power set of a countably infinite set must have a higher cardinality than the countable infinity, ℵ0. And the exponential formulas prove that the cardinality is indeed 2ℵ0 or ℵ1. Instead of disproving George's discovery of the non-countable infinity, you've just proven it!
You see, George's friends say wearily, the whole point is that you can't assume properties of infinite sets are the same as those of a finite set. We repeat: Just because a finite set has a property for any number n, no matter how high, that doesn't mean the infinite set must have that property as well.
Ha? ask the Intuitionists (quoting Shakespeare). C'mon. For all his discoveries, George Cantor never even proved there are infinite sets. Modern set theory has to make that an axiom. You can prove anything if you assume it to be true. So George did nothing.
Did nothing? hoot George's friends. George just gave the world a rigorous definition for actual infinities - that is, infinite sets which have a complete existence, not just (ptui) "potential" infinities. The limiting of mathematics to constructive proofs is confusing abstract mathematical concepts with conclusions of the finite physical world. So why don't you just take your constructive proofs and ...
Well, let's just say that to this day George and the Intuitionists don't agree.
A Useful Application
That said, today the majority of mathematicians accept the Law of Excluded Middle even for infinite sets. That's because you can prove more things with the Law of Excluded Middle than without it. And it just leads to too many interesting - and some say profound - conclusions about the world.
For instance, don't you think it would be great to prove there are true statements that cannot be proven? Certainly a lot of clergymen, politicians, and parents would like to think so. And if we accept the diagonal argument, we can do just that.
Remember we've proven that there are more real numbers than counting numbers and that the subset of all counting numbers is also not countable. And with George's work we now set out to prove there are more truths in the universe than we can prove.
But first we need to decide what it means to prove something. And to do that we need to know what we mean by a theorem.
In math or logic, when you want to prove something you have to start with a set of premises. In math these are axioms or previously proven theorems. Then by deductive reasoning you arrive at your conclusion.
Now if you do this right, each step of your reasoning is either an axiom, a previously proven theorem, or a new statement derived (correctly) from one or more of the previous steps. Eventually (if you're correct) then the last step in your line of reasoning will be the final conclusion you want. That last line is the theorem. The whole list of symbols from top to bottom is your proof.
The simplest and most boring "proof" in the history of mankind began with Aristotle. But it shows the difference between a proof and a theorem.
| All men are mortal. |
| Socrates is a man. |
| Socrates is mortal. |
In this case the theorem is the final sentence. "Socrates is mortal." That's what you have proven. The proof is the list of sentences that lead to the final statement.
In essence then a proof is a list of statements arrived at by a given set of rules. Whether the theorem is in English or another "natural" language or is written symbolically doesn't matter. What's important is a proof has a finite number of steps and so uses finite number of symbols.
Now it is true that the number of symbols is open ended. If you don't want to use English you can use mathematical and logical symbols. In that case, you can have an unlimited number of variables which can be written as x0, x1, x2, ... and so on forever.
But at most we can only use a countably infinite number of symbols. So any theorem must be shorter than a countably infinite number of steps and the limit of symbols is likewise countably infinite.
So no matter how many theorems we prove, books we write, or politicians give speeches, the symbols used will always make at most a countably infinite list. So at most there are only a countably infinite number of mathematical theorems and so only a countably infinite set of proofs.
So now as the $500 an hour psychiatrist said after a year of twice a week sessions, we can begin, yes?
OK. Let's take the set of counting numbers and make the power set. That is, we make all possible subsets of the counting numbers.
Then pick a number, any number. We'll pick the number "1". Then for every subset it will be either true or false that "1" is a member of that particular set. So there is at least one true mathematical statement associated with each subset of the counting numbers.
But wait. How many truths do we have? Well, we have just shown that the number of subsets of the counting numbers is uncountably infinite. So there must be an uncountable number of true mathematical statements.
But remember what we said above? We only have a countable number of theorems. So:
 |
There are not enough theorems to prove all the true mathematical statements. |
Yes, Virginia, there are true mathematical statements that can't be proven.
How about that?
References
Georg Cantor: His Mathematics and Philosophy of the Infinite, Joseph Dauben, Princeton University Press, 1990.
Galileo: Two New Sciences, Galilei, Galileo, Stillman Drake (Translator), University of Wisconsin Press, 1974.
"A Crash Course in the Mathematics Of Infinite Sets", Infinite Reflections, Peter Suber, Peter Suber. Department of Philosophy, Earlham College, Published in St. John's Review, Volume 44, Issue 2, 1998, pp. 1-59.
"Constructive Mathematics", Stanford Encyclopedia of Philosophy, Tuesday, November 18, 1997 (Revised: Wednesday, May 30, 2018.
"Constructive Mathematics", Douglas Bridges and Erik Palmgren, Stanford Encyclopedia of Philosophy, Tuesday, November 18, 1997 (Revised: Wednesday, May 30, 2018).
"Intuitionistic Logic", Joan Moschovakis, Stanford Encyclopedia of Philosophy, Wednesday, September 1, 1999 (Revised: Tuesday, September 4, 2018).
Metalogic: An Introduction to the Metatheory of Standard First Order Logic , Geoffrey Hunter, University of California Press, (1973).
As hard as it is to believe, there are many people who think that the CooperToons Merry Histories and Educational Essays are written in a spirit of sarcasm and in fact are satires of scientific, philosophical, and theological writings. But a quick perusal of Geoffrey's book (just the first chapter for crying out loud) will show you that the proof given in such painful length and detail above is essentially that which Geoffrey gives us with much less wind.
Geoffrey's book is intended for people who have some introduction to formal logic but otherwise its for the layman who is interested in going beyond the "Socrates is mortal" type schtick. As he points out, if you take a logic course in college they usually end before you get to studying the interesting stuff.
An alternative proof, by the way, to show there are true statements with no proof is to realize you have specifiable sets which can be expressed as a formula, and there are other sets which cannot be specified as a formula.
For instance the set of even numbers, E, is defined as:
E = {x: x = 2n where n = 1, 2, 3, ...}
This is read as "The set E is the set of all x such that x = 2n where n = 1, 2, 3, ...
So in general a set, S, is specifiable if you can write it like:
S = {x: P(x)}
where P(x) is a formula you can plug x into and get a member of the set.
Now you can only prove an element is in a set if the set is finite - which means you can check each element if you have the time - or if you have a formula for determining if the element satisfies the equation. But there are only a finite number of formulas or at best a countably infinite number of formulas. As we showed there are uncountably infinite sets, there are sets without an associated formula and yet are infinite. So you there are some sets where you can't tell if a given number is a member or not - even though it is. So once more we have more true mathematical statements than we have proofs.
Dangerous Knowledge, BBC, 2007, Internet Movie Data Base.