Paul Cohen, Georg Cantor, and the Continuum Hypothesis

Although Coopertoons would never expect enthusiasts of Howard Stern, Spike TV, or WIP Sports radio to know about Paul Cohen, others have been continually (and that's a joke, by the way) hounding CooperToons about him. "Forget about Elvis, Paul Newman, or Steven Spielberg!" they say. "When are you going to put up a caricature of Paul Cohen?"

All right! CooperToons cannot withstand the pressure. So here's the drawing, for crying out loud. Sheesh!

Now just in case any enthusiasts of Howard Stern, Spike TV, or WIP Sports radio are reading this (a low probability occurrence we admit), CooperToons will say that Paul was the Stanford mathematician who proved - yes, proved (and may we all die the deaths of dogs if we lies) - that THE CONTINUUM HYPOTHESIS WAS INDEPENDENT OF THE OTHER AXIOMS OF SET THEORY!

Whew! I don't know about you, but I was getting worried.

Of course, even the most dense of enthusiasts of etc., etc., who are reading this, surely know what the continuum hypothesis is. But again for that small minority of the world's inhabitants who live with their heads buried in the sand or fixed to the satellite dish, we have to start out by saying to understand the continuum hypothesis, you have to think about infinity. More specifically, you have to realize that all infinities are not created equal.

The concept of infinity itself is pretty old, going back to the Greeks (Aristotle talked about it a lot). The big debate was if infinity should be thought of as a number. Some said yes, others, no. The brouhaha went back and forth until the 19th century. Then a German mathematician named Georg Cantor (pronounced GAY-org, but we can call him "George") put infinity on what they (i. e., mathematicians) call "mathematical rigor". George said no, infinity is not a number. It is a concept. But George said, infinity is a concept with properties that can be precisely stated. But what was most important was he identified two kinds of infinity and proved there was an exact mathematical relationship between the two.

The simplest of infinities was (and still is) that of the natural (i. e., counting) numbers. Simply put, consider a set in which the elements can be ordered. Then pick a number, any number. If no matter how high a number you pick there is always another element one step above the element you picked, then you have an infinite set. Such an infinity, George said has the size of the set of counting numbers. Calling a spade a spade, George labeled it a countable infinity. In other words, the property of there always being a number above any other that we pick - that is, that every counting number has a successor - becomes the defining property of a countable infinite set. Any set that is the same size as the counting numbers is also countably infinite.

But what does it mean if an infinite set has the same size as another. Since the size is infinite, you can't assign a number to the sets. After all the counting numbers go on forever.

N = { 1 , 2 , 3 , 4 , ..... }

 

Like we said, no matter which number you pick, you can always add one to it and get another number. But the way to tell if any set has the same size as another set simply see if you can put the elements into a 1:1 correspondence. For instance, the set of counting numbers is clearly not the same size as the set {1, 2, 3} because you can't put the elements of the two sets into a one-to-one correspondence.

1		1
2		2
3		3
4		Oops! Ran out of numbers!
5		.
6		.

 

Or to put it in everyday terms, you have more than three counting numbers.

However, you can put the sets {1, 2, 3} and {4, 5, 6} into one-to-one correspondence. It's easy enough to show:

1		4
2		5
3		6

 

Or more precisely, you can create a new set of pairs where each of the elements are grouped without repetition.

N = { {1, 4} , {2, 5} , {3, 5} }

 

So if you can set the elements of two sets into 1:1 correspondence, then you know the sets are same size and the size is the number of pairs in the new set. Since the size of a set is specified with a cardinal number, George termed the set size its cardinality. To determine the cardinality of a finite set is easy. Simply count the elements. So the two sets {1, 2, 3} and {4, 5, 6} have a cardinality of 3. Again reverting to everyday language, there are three elements in each set.

But with infinite sets you have a bit different scenario. Although there is no real number for the size of an infinite set, it is still possible to put some infinite sets into a one-to-one correspondence. For instance the counting numbers and even numbers can be paired up easily enough.

1		2
2		4
3		6
4		8
.	.	.
n	.	2n
.	.	.

Or more precisely you can create a new set, P, defined by:

P = { {n, 2n} where n = 1, 2, 3, ...}

Since these two infinite sets can be put into one-to-one correspondence, they must, according to George, have the same cardinality just like finite sets can have the same cardinality. And that was George's first big and somewhat paradoxical discovery. Since the set of even numbers has the same cardinality as the counting numbers that does mean that half of the counting numbers is just as large as the whole set of counting numbers. And the set of all integers - that is positive and negative whole numbers (including zero) - can also be matched up in a 1:1 correspondence with the counting numbers.

1		0
2		-1
3		1
4		-2
5		2
6		-3
7	.	3
.	.	.
.	.	.

This can be put a bit more formally as:

Odd Numbers:	(n - 1)/2
Even Numbers:	-n/2

Or even more formally as the set of ordered pairs:

N = { {(n, (-1)⁽ⁿ⁺¹⁾n/2 - [(1 - (-1)⁽ⁿ⁾])/4} where n = 0, 1, 2, 3, ...}

which is the same as the more familiar algebraic notation:

f(n) = (-1)⁽ⁿ⁺¹⁾n/2 - [(1 - (-1)⁽ⁿ⁾])/4

(Like the commercials say, try this formula. It really, really works.)

So doubling (and doubling plus one) of a countable infinity is still a countable infinity. In a nutshell, then, for a countable infinity, the sum is the same as the parts - as long as the parts are also infinite.

Now George realized there was no actual number for the cardinality of the counting numbers. Rather than use the old Ben Casey "Man - Woman - Birth - Death - Infinity" infinity (that is, 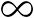), he designated this infinity as 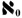(called aleph-null). So far so good.

But then George stumbled onto another discovery. Some infinite subsets are smaller than the infinite set that they came from. This means there are some infinities larger than others. For instance, the set of real numbers - which includes all the counting numbers, negative integers, zero, rationals (fractions), irrationals (like the square root of 2 and our old friend, π) - can not be put into a one-to-one correspondence with the counting numbers. And as you might suspect, the larger infinity is that of the real numbers. George proved his new discoveries conclusively by inventing the diagonal argument or the diagonal proof. (Since this proof is perhaps even more important that the famous Pythagorean theorem, CooperToons feels obligated to provide an explanation which you can view in a new window if you click here.)

Since the two infinities were not the same, George designated the infinity of the real numbers as 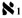(called aleph-one). But he tried to go further relate the two infinities to each other as if they were numbers.

More exactly, he believed the relationship was was exactly the same for calculating the number of subsets you can create from a set.

For instance, take our old friend, the set { 1 , 2 , 3 }. Now take all combinations of the numbers and put them into sets. What you have is:

 

{ 1 } , { 2 }, { 3 }, { 1 , 2 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 }

 

Notice that there are 7 sets. In other words, if you have a set with three members you can make 7 sets or 2³ - 1 sets. To make things nice and easy (yeah, right), mathmeticians say the empty set {}, that is a set with nothing in it and most often represented by 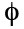should also be counted as a subset. That makes of eight sets from a set of three elements. So if you have a set of n elements you have a total 2ⁿ subsets.

In short George thought 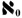and 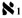were related in the same way. That is,

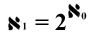
George tried to prove this relationship but couldn't. So a lot of people aren't surprised to learn at this point George went nuts. Some popularizers of George's life (like a fairly recent BBC special) imply all this thinking is what did it. In reality, George's problems likely had an underlying medical cause.

More generally George believed there was no infinite set which had a cardinality between 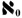and 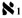. This is the continuum hypothesis and people kept trying to prove it for many years after George died in 1918.

The resolution of the continuum hypothesis problem got a shot in the arm in 1940 when Kurt Godel came along. Kurt had already gained fame in 1931 by proving that there were true things in mathematics you can't prove (well, that's sort of what he proved). But now he demonstrated that you could not disprove the continuum hypothesis from the axioms of set theory.

That's where Paul came in. In 1963 and 1964, he published two papers in the Proceedings of the National Academy of Sciences where he proved that the negative of the continuum hypothesis also did not produce a contradiction in set theory. So when you combine Paul's discovery with Kurt's, this means the CH is independent of the other axioms, much like Euclid's fifth postulate is independent of Euclid's other four. So if you wish, Paul said, you can have an extra infinity between the infinity of the counting numbers and that of the real numbers. It's really up to you, although a lot of mathematicians still keep arguing about it, or at least how to create a set with that type of infinity. In any case, for his discovery, Paul was awarded the Fields Medal, which because there is no Nobel Prize in mathematics, is often called the Nobel Prize of Mathematics.

At this point the enthusiasts, etc. etc., can claim all this is a bunch of intellectual hooey. Since we live in a finite world - the number of atoms in the universe is large but still finite - then all of these theorems have no real applications for someone whose greatest dilemma is to decide how to maximally utilize the time between commercials while watching the NFL playoffs. All the fun stuff in math disappears if you don't have infinity. After all, with infinity can you prove there is a bucket of paint that can hold a bit more than three gallons of paint but you can never have enough paint to paint the bucket (this is the famous paradox of Torricelli's Trumpet , but it really should be called Torricelli's Bucket and it isn't really a paradox). And take the Banach-Tarski theorem (please). This says as long as you can slice a sphere into a sufficiently large number of properly selected shapes, you can then move the parts around and reassemble them into two new spheres, both of which are the same size as the original. The trouble is the theorem doesn't work for spheres made up of real atoms. So forget about getting two balls of gold for the price of one.

Still some people like the idea of infinity, and so Paul certainly helped us there. But best of all Paul's discovery was a boon to literature . After all, without him we would never have the deathless verse:

There once was a man named Paul Cohen
Who in the field of mathematics was mowin'.
George a question surmounted.
Two infinities he counted.
But with Paul they just kept a growin'.

References

Paul's two papers are on-line at http://www.pnas.org/content/50/6.toc and http://www.pnas.org/content/51/1.toc. These links open to the tables of contents of the Proceedings of the National Academy of Sciences and Paul's articles can be viewed by clicking on the .pdf icons at his article listings. Tough going even for the mathematical cognoscenti (but bravo! for open access).

A good website with a brief discussion but good references is http://www.statemaster.com/encyclopedia/Continuum-hypothesis. The two articles in the references from the Notices of the American Mathematical Society are particularly useful.

Paul's proof was by his forcing method which remains an abstract and difficult technique to learn. Although there are various web articles which attempt to explain the technique, none are entirely satisfactory since you need to know considerable mathematical jargon just to get started. Sadly there is nothing along the lines of "Godel's Proof" by James Newman and Ernest Nagel (New York University Press, 1958, revised edition, 2001) for Paul's work.

Oh, yes. It is possible to paint the inside of Torricelli's trumpet (or bucket) if you define "to paint" properly. That is, if you treat painting as coating a surface with a film of finite thickness. By clicking on the link you can learn a bit more about Torricelli's trumpet and its quirks.