|
|
|
A Most Merry and Illustrated Proof of Cantor's Theorem on the Countability of Rational Numbers
A Most Merry and Illustrated Proof of the Unintuitive
George was not being irrational.
Perhaps it's a sad commentary on higher education in the United States, but CooperToons has actually been referenced by academic websites. Sometimes - like the Coopertoons essay on the life of folklorist Vance Randolph - they have even been recommended reading for university courses. CooperToons even found a reference on an Ivy League website, for crying out loud!
But what's even more amazing is that students have found the information useful. One math student wrote that the CooperToons essay on the diagonal argument was the first comprehensible explanation of the topic he had read. Another CooperToons first!
Sadly for the further education of our youth, it was this positive feedback that egged CooperToons on to attempt an explanation of how the number of counting numbers (1, 2, 3, 4, ... ) is the same as the number of integers ( ..., -3, -2, -1, 0, 1, 2, 3, ... ). This theorem, like the diagonal argument, was first proven by the great German mathematician Georg Cantor, who although you really pronounce his first name as "GAY-org", we - being friends - will call George.
But George didn't stop there. He decided to count how many rational numbers there were. At that time just about everyone thought there had to be a lot more rational numbers than integers. But George wasn't so sure. If you could count the integers, then why couldn't you count the rationals as well?
How George Did It
Before going into how George counted rational numbers, we'll review a bit about the actual technique George used. It was essentially the same method he used to count the integers. In both cases, George was trying to count infinity, and at the time, no one was quite sure what infinity really was.
The nature of the infinite is a topic that goes way back to the ancient Greeks. Aristotle probably gave it the most thought, and his definition anticipated the modern notions pretty well. But it wasn't until George began inventing set theory that he really identified the essential properties that characterized an infinite set.
The problem with counting infinity, George realized, was no one had yet defined it strictly in mathematical terms. Nor did he did assume there was only one kind of infinity. But if there were different infinities, then he realized simplest infinity had to be the infinity of the counting numbers.
So the first question he asked was how do we really know the counting numbers are infinite? That can still be an exasperating question to a teacher when it's raised in a middle school math class. But fortunately, George had the answer.
We know the counting numbers are infinite, George said, because no matter what number you pick, you can always add one to the number and get another number. This is not just one characteristic of an infinite set, George said. It is the actual definition. George called this simplest of all infinities - the infinity of the counting numbers - a countable infinity. George was the type of man who called a spade a spade.
George then figured out how to tell if other sets were countably infinite. First assume you pick a counting number as large as you like, and you find it corresponds to an object of the set in question. Now if there is always another number larger than the one you just picked that also has a corresponding element of the set, then the set is just as large as the counting numbers - ergo, it is also countably infinite.
In short, George said, any set whose elements could be put into a one-to-one correspondence with counting numbers was also countably infinite. Such a correspondence is a simple extension of how we know finite sets are the same size. After all, if you count a set, you are simply making a one-to-one correspondence of a subset of the lowest possible counting numbers with the objects of the set. The highest counting number you use is the size of the set. But if there is no highest number, your set is infinite.
But infinity - even a countable infinity - is not a number in the usual sense, and George's suspicion that there was more than one kind of infinity was also correct. He later proved there was an uncountable infinity using the diagonal argument. George also hypothesized there was an absolute infinity that was the highest infinity of all. All infinities shorter than this highest infinity George termed transfinite numbers. The smallest transfinite number - the size of a countably infinite set - George named aleph-null or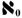 
. So if you were able to prove that a set was of size 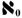, you were actually counting an infinite set.
But 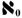is not just a large counting number and so sets which are 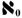in size have some unusual properties. The properties are so unusual that some people didn't believe George's conclusions, and even today some people have trouble accepting that what George hath wrought.
For instance, a set you think would be half the size of the counting numbers may really be just as large. You can see this is true since you can pair up the counting number with the even numbers.
2
2 4
3 6
4 8
.
.
.
So no matter what even number you pick, it is associated with a unique counting number. This pairing is shown more exactly by taking a simple function which takes every counting number and generates the even number.
f(n) = 2n where n = 1, 2, 3, ...
In general, then, some proper subsets of infinite sets,were in fact, infinite.
George didn't stop there. He said some sets that seem larger than the counting numbers are also the same size. He did this by showing you could match up the integers with the counting numbers:
0
2 -1
3 1
4 -2
5 2
6 -3
7 3
.
.
.
The one-to-one correspondence is exactly expressed by an admittedly somewhat complex formula.
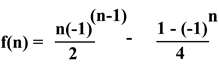
where n = 1, 2, 3, ...
This formula was proven by mathematical induction showing that every counting number is associated with a unique integer. Hence the two sets are the same size.
This then was the key to counting infinite sets. As long you can find a function that maps any counting number, no matter how large, to a unique element of another set, then the other set is the same size as - or as George put, has the same cardinality - as the counting numbers. Any such set is itself countably infinite.
Now with the rules set in place, George decided to tackle the sticky problem of the rational numbers.
The Rationale of the Rationals
When people began to get serious with numbers, they realized you needed something more than integers. After all, there were times when you had to deal with parts of a number. Eventually, then, someone - particularly the Babylonians and the Egyptians - developed the concept of fractions or more exactly, the rational numbers.
Rational numbers are best represented as ratios of integers (the word rational refers to the ratios, not anyone's ability to reason). Integers are also rational numbers as they can be represented as ratios (0/1, 1/1, -1/1, 2/1, 3/1). But the other rational numbers fill the spaces in between the integers. For a while a lot of people (mostly the Greek philosophers) thought that the rational numbers were all the numbers you needed. And for the practical purposes of everyday problems, they were right. Even today computers use rational numbers in all their calculations, even when using formulas that involve irrational numbers like π and e. After all, any irrational number that is rounded off becomes a rational number, and if you want to measure the circumference of a circle, depending on how accurate you wanted to be, you can multiply the diameter by 3, 22/7, 355/113, or 314159265358979/100000000000000. But in trying to count the rational numbers, you encounter a property they have that is not shared by integers. Rational numbers are dense. That is, if you pick any two rational numbers, you can find another rational number between them. That also means that if you pick any two rational numbers, you can pack any number of other rational numbers between them. So it seems there has to be more rational numbers than integers. But that's what people thought abut the integers, too, and when George set out to count the rationals, he was not being irrational. A Rational Arrangement Like George's proof about the integers, you can find all sorts "diagrammatic demonstrations" that rational numbers are countably infinite. One such - quote - "proof" - unquote - is shown below. The idea is if you follow the arrows you'll find all the rationals you want, and there's always a matching counting number for every rational.
A - Quote - "Proof" - Unquote
This diagram really doesn't prove the case, of course. For all we know the set of rational numbers grows faster than the counting numbers, and all we're doing is matching up only the first few elements of each set. What we need is a formula which will match every rational number to every counting number. If we can find such a formula, then the two sets must be the same size.
But first, we'll begin at the beginning and decide exactly what rational numbers are - or rather how to best represent them.
Rationals have two popular representations. One is as the ratios we showed above (1/2, 1/9, 4/33, etc.). The other notation is as a terminating or repeating series of digits (0.5, 0.111111..., 0.12121212...).
On the other hand, for our purposes, the best way to represent rationals are as ordered pairs of the integers. Ordered pairs are simply two numbers in a particular order, usually represented in parentheses like, (1 , 2), (1 , 9) or (4 , 33). For these to be rationals, then, the first number is the numerator and the second is the denominator.The notation fits with the problem which is to find a function that takes an ordered pair, (i , j), and generates a unique counting number.
f(i, j) = n where n = 1, 2, 3, ... and i and j are integers.
This type of formula - with some restrictions - will establish the one-to-one correspondence we need.
Now, as the psychiatrist said, we can begin, yes?
Some Definitions
Definitions are commonly used in proofs. Kurt Godel in his famous theorem on undecidability devised a whopping 46 definitions where each successive definition was dependent upon the previous one. The purpose of definitions is they can simplify a proof although it may not seem like it in Kurt's theorem.
But the nice thing about definitions is you really don't have to prove anything. A property of numbers from a definition follows immediately from the definition. In fact, in a lot of proofs the writer will say something like "And so our conclusion comes directly from our definition which as all but the most dense can readily see." However, for the sake of clarity we'll try to give a bit more elaboration - probably so much elaboration that we will insult the intelligence of all but the most dense.
As the diagram above suggested, we need to come up with an arrangement of rationals that can be listed in a sequence. In doing so we will produce a proof in three parts:
1. First, as we said above, the rational numbers are defined as ordered pairs of zero and counting numbers.
0 = (0, 1)
1/2 = (1, 2)
3/4 = (3, 4)
1/32 = (1, 32)
Here we note we have to exclude pairs like (1, 0) since 1/0 is not defined as a rational number (you can't divide by zero). That is, no ordered pair has the second digit as zero.
Now we also need to address how distinct we want to be. That is, 1/2 is a rational number. But so are 2/4 and 50/100. The last two rationals have the same value as 1/2, yes. But should we treat these as different rationals?
Because of the original definition of rationals - ratios of integers - we will treat such numbers as distinct as long as they have different integers. That is also in keeping with the original use of rational numbers and permits greater specificity in what they represent. For instance if you have a parcel of land and divide it into two sections and award one of those to Euripides for his bravery in the Peloponnesian War, then you have given him one half of the land. But suppose you have the father and son, Strepsiades and Pheidippides, who were both valiant in battle, but you don't have enough land to go around for another war hero. In that case, you divide the land into quarters and award one parcel each to Strepsiades and Pheidippides. So you have given two of the four sections to the family and now have one-half of the original land left over for someone else. So by our definition, 1/2 and 2/4 are different rational numbers, although they do have the same value.
Oh, yes. Letting numbers like 1/2 and 2/4 be different rationals simplifies the proof.
2. The second part of the definitions is to define the arrangement of the rationals in a set of rows. This is very simple. For any row n, the kth ordered pair is (n - k, k) where k is 1 to n.
Which means each row appears as:
Row n: (n - 1, 1), (n - 2 , 2), (n - 3, 3), ... , (0, n)
In other words, any row, n, starts off by having the first ordered pair as (n - 1, 1). Then we calculate the next ordered pair on the same row by subtracting 1 from the first element and adding 1 to the second. We continue the process until we end up with the last ordered pair on a row as (0, n).
1: | (0, 1) |
2: | (1, 1), (0, 2) |
3: | (2, 1), (1, 2), (0, 3) |
| . |
| . |
| . |
n: | (n-1, 1), (n-2 , 2), (n-3, 3), ... , (0, n) |
n+1: | (n, 1), (n-1 , 2), (n-2, 3), ... , (0, n + 1) |
| . |
| . |
| . |
There are two properties of our array that we will mention here. First, all ordered pairs in any column have the same value for the second element. That is they have the same j value.
Next, our array generates only the positive rationals and zero. But we will be able to show that it is easy (or relatively easy) to slip in the negative rationals and that the final formula we create will generate all the positive and negative rationals.
That's all there is to our definitions. Now we will start off our proof by pointing out some other properties of the definitions, some of which require a little bit of proof but not too much.
Starting the Proof
George's proof has two main parts which we outline briefly.
1. We first prove our definition generates all rational numbers.
2. We then show we can use the array to derive a formula where the ordered pairs generate all the counting numbers.
If we prove both of these points, we have proven what we want to prove - that the counting numbers and rationals have one-to-one correspondence and the two sets are the same size.
Now, to proceed.
From the definition of our array, there are three conclusions we can draw.
1. The number of pairs in a row is equal to the row number.
This does follow immediately from the definition. The second element of the pair starts with 1 and increases until it reaches the value n. So there's n elements per row.
| n: | (n-1, 1), | (n-2 , 2), | (n-3, 3), | ... , | (0, n) | ||||||
| | | | | ||||||||
2. All rational numbers are generated by our definition. Specifically, you will find for any ordered pair, (i, j), on Row i + j and Column j.
People familiar with arrays probably recognize that such a definition necessarily generates all possible ordered pairs. But for those who don't see it right away, you first note that if move down to any row j, the last ordered pair is (0, j). Then stay in the same column and you can eventually find any i value you need. So when you can find any ordered pair is (i, j), you have to be in Column j, and Row i + j
Or in diagrammatic form:
For example, you want ordered pair (31415926, 271827)? Easy. Move to row 271827. The last ordered pair is (0, 271827). Count down 31415926 places, and you will be in row 271826 + 31415927 = 31687753. Sure enough, your ordered pair will be (31415926, 271827)
1: (0,1)
2: (1, 1) (0, 2)
3: (2, 1), (1, 2) (0, 3)
.
.
.
31415927: (31415926, 1), (31415925 , 2), ... (0, 31415927)
.
.
.
31867753: (31867753, 1), (31867752 , 2), ..., (31415926, 31415927), ..., (0, 31867753)
3. Each ordered pair is unique; no ordered pair is repeated.
Again people who are familiar with arrays say this - quote - "follows immediately from our definition" - unquote. But eins mehr (as George would say), if the conclusion isn't obvious, then consider the following.
From the way we defined our array, we pointed out that the columns share the same j value. So if two ordered pairs are identical, then they must be in the same column.
But that isn't possible. From the way we defined the rows, for Row n, the ordered pair in column j is (n - j, j). Go up or down any row x places and the ordered pair is (n ± x - j, j). So you can't have the same i value if you are in the same column.
n: | | |||||
n + 1: | |
So by our definition, all ordered pairs are unique, and our array represents all the possible (positive) rational numbers.
Now we can proceed with the Proof Proper.
The Proof Proper (or the Proper Proof)
The final steps remain to develop a real algebraic formula relating the counting numbers with the ordered pairs, and hence the rational numbers. There are five steps to this last part of the proof and all are based on how we constructed our array.
1. The total number of ordered pairs up to and including Row n is n(n + 1)/2
The number of ordered pairs in each row is n. So we need to sum up the counting numbers from 1 to n.
| Total ordered pairs = | 1 | + | 2 | + | 3 | + | 4 | + | ... | + | n |
| Up to Row | 1 | 2 | 3 | 4 | ... | |
Our formula, then, follows from the well known formula available in any mathematics reference source.
1 + 2 + 3 + ... + n = n(n + 1)/2
This is also a good example of something that can be proven easily by induction but we will let that pass for now.
At this point, it might be tempting to declare victory and with a bit of handwaving, we could. After all, we have made a formula which counts the order pairs in our array. But it is not a formula that explicitly relates a particular rational number to a specific counting number. Also we have so far still restricted our array to positive rational numbers and zero. So - as an American president once said - let us continyeh.
2. The numbers of ordered pairs up to the row before the row with ordered pair (i, j) is (i + j - 1)(i + j)/2.
Remember for every row, n = i + j for any ordered pair in the row. Therefore the previous row is n - 1 which is equal to i + j - 1. Using the formula we just derived, the total number of ordered pairs up to and including row i + j - 1 is
| n(n + 1)/2 | = (i + j - 1)(i + j - 1 + 1)/2
| | = (i + j - 1)(i + j)/2 | |
3. For an ordered pair (i, j), the number of ordered pairs in the same row up to and including pair (i, j) is simply j.
Once more this conclusion is immediate from our definition. You start counting in the first column where j = 1. So regardless of the row when you reach any number, j, it is in place j.
4. The total number of ordered pairs up to any pair (i, j) is (i + j - 1)(i + j)/2 + j
This follows simply by adding the numbers from the previous two steps:
Total pairs = (i + j - 1)(i + j)/2 + j
N(i, j) = (i + j - 1)(i + j)/2 + j
and N(i,j) has the values 1, 2, 3, ...
At this point, readers of the previous essay on counting the integers, may wonder if we now have to prove this equation by mathematical induction. The answer is no because we did not get this equation by a mixture of empiricism and guesswork. But here we derived this equation by starting with our definitions, and then by using proper mathematical deductions, we came up with the formula. That process constitutes a proper proof - a constructive proof, in fact - and so we don't need to do any more.
But oh, yes. We've only completed half the proof.
Adding the Other Half
Yes, we have derived a formula that relates positive rationals to the counting numbers. At this point we could simply say you can derive an analogous equation using negative j's which would correspond to negative rational numbers. We do this by changing the plus sign before the j's with minus signs, and then the ordered pairs (i, -j) will generate the counting numbers. Then we say that if you combine two countable infinities you still have a countable infinity. So we have proven all rationals are countably infinite.
While correct as far as it goes, the more finicky of theorem provers may want to know whether we can make one formula that fits the bill and generates all rationals - positive, negative, and zero - and matches them with the counting numbers. The answer is yes or we wouldn't have raised the question. The Big Formula The trick to making space in the counting numbers for both positive and negative rationals is to realize that if you multiply any counting number by 2, you get an even number. Multiply it by 2 and and subtract one, you get an odd number. So take our formula (as Henny Youngman might have said, please).
N(i, j) = (i + j - 1)(i + j)/2 + j
Multiply the right hand side by 2 and our array of ordered pairs, (i, j), will generate the even numbers only.
| NEven(i, j) | = 2[(i + j - 1)(i + j)/2 + j] |
| = (i + j - 1)(i + j) + 2j |
To generate the odd numbers, we multiply our original equation by 2 and subtract 1.
| NOdd(i, j) | = 2[(i + j - 1)(i + j)/2 + j] - 1 |
| = (i + j - 1)(i + j) + 2j - 1 |
Now we have to make one of the equations work for a negative j. We'll use the even numbers as we outlined above - just put a negative sign before j.
| NEven(i, j) | = (i - j - 1)(i - j) - 2j |
Now we we cannot simply add the two equations, NOdd(i, j) and NEven(i, j). Instead first we need to multiply each one by a mathematical "switch". That is, we multiply NEven(i, j) and NOdd(i,j) by a factor, that that will turn off part of the equation depending on whether j is negative or not. That's really pretty easy.
The formula
(1 - j/|j|)/2
has a value of 1 if j is negative and 0 if j is positive (|j| represents it usual meaning as the absolute value of j).
Similarly, the formula
(1 + j/|j|)/2
gives us a factor of 0 if j is negative and 1 if j is positive.
So now if you multiply the separate equations, NEven(i, j) and NOdd(i, j) by the appropriate factors and then add everything together, you get one equation that really, really works.
N(i,j) = [(i + j - 1)(i + j) + 2j - 1](1 + j/|j|)/2 + [(i - j - 1)(i - j) - 2j ](1 - j/|j|)/2
This, equation will indeed produce the counting numbers if you take our original array and insert the ordered pair with the negative j under it's positive counterpart.
| (0 , 1): | 1 | |
| (0 , -1): | 2 | |
| (1 , 1): | 3 | |
| (1 , -1): | 4 | |
| (0 , 2): | 5 | |
| (0 , -2): | 6 | |
 | ||
| (i , j): | n | |
| (i , -j): | n + 1 | |
|
Some people,though, still don't like saying the multiple zeros (0/1, 0/2, 0/3, etc) are distinct rational numbers. Yes, you can argue that 2/4 - that is two parts out of four - may in different contexts be distinct from 1/2, 3/6, 50/100, and the like. But zero is zero and we don't want the repetitions.
But there is an alternate formula - whose proof, as the textbooks say, is left for the reader - that omits the repetitions. [The proof, by the way, is based on defining the rows so that Row 1 is (0,1) and starting with Row 2 the rows end with (1, n), not (0, n). That Row 1 and Row 2 both have one ordered pair complicates the algebra, but not all that much.]
N(i,j) | = [(i + j - 1)(i + j - 2) + 2j + 2δ0,i - 2](1 + j/|j|)/2 |
| + [(i - j - 1)(i - j - 2) - 2j + 2δ0,i - 1](1 - j/|j|)/2 |
| + 1 - δ0,i |
where δ0,i is the famous Kronecker delta where
δ0,i = 0 if i = 0
and
δ0,i = 1 if i ≠ 0
This formula, then, will map all the rational numbers to a unique counting number. Exactly what we wanted.
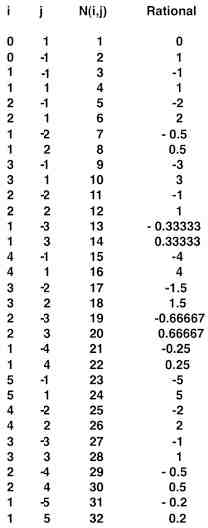
The Integers and Counting Numbers
In other words, there sure enough is a one-to-one correspondence with the rational numbers and counting numbers. The two sets must be the same size.
Once more we have to tip our hats to George.
A Point of Clarification
At this point, some people remain unconvinced. After all, they say they can match the rationals 1/1, 2/1, 3/1, 4/1, with the counting numbers and have an infinite number of rationals left over. Therefore there must be more rationals than counting numbers. You can make the same argument for the number of integers being more than the counting numbers. You can match the positive integers, 1, 2, 3, ..., etc., with counting numbers and so have the negative integers (and zero) left over. So how can integers, rationals, and counting numbers be the same size?
Not so fast, there, Pilgrim. Yes what you say is true, but completely irrelevant. When you say 1/1, 2/1, 3/1, 4/1, etc,. can be matched with counting numbers that is certainly the case - because 1/1, 2/1, 3/1, 4/1, etc. are indeed the counting numbers. So all you are saying is the counting numbers can be matched with the counting numbers. Or in other words, when you do your one-to-one correspondence, you are simply omitting to match up all the members of your set with the other set.
On the other hand, if you want to say the set of rationals is not the same size as the counting numbers, you must prove that no function will give us a one-to-one correspondence to rationals and counting numbers. Only if you can prove no such pairing exists, then can you correctly claim the sets are not the same size.
But what we just proven, both for the rational numbers and as we did earlier for the integers, that there are indeed such functions. So the sets of rationals, integers, and counting numbers must be the same size.
Q. E. D.
Schaum's Outline of Boolean Algebra and Switching Circuits, Elliott Mendelson, McGraw-Hill, (1970). Problem 2.18 on page 46, is a worked example which gives the formula to formula relating positive rationals to the counting numbers. As usual, if you want information about a particular topic, it's hard to beat a Schaum's Outline.
Georg Cantor: His Mathematics and Philosophy of the Infinite, Joseph Warren Dauben, Princeton University Press (1990). Not really a biography and not something for the general reader (knowledge of fairly advanced math expected). You'd think by now George would have a real biography. True many mathematicians don't leave incredibly exciting lives, but you'd think someone like George deserves better.