The Problem with Pyrene
Or How PMO's Parameters Pour Forth Powerful Possibilities for Potentially Perplexing Problems
(Or the Real Hückel's Rule)

Michael To the Rescue?
As this writer (and illustrator) was seeking further resources to bring education and enlightenment to the world, he found a note posted on the Fount of All Knowledge. It seems a student was taking an organic chemistry course and had encountered the famous 4n + 2 rule for determining if a compound is "aromatic". As all know, having 4n + 2 π electrons in a ring is a defining characteristic of aromaticity.
So why, the student asked - and it was a true cri de coeur - is pyrene - which has 16 π electrons - that is, 4n electrons - considered an aromatic compound?

To say the posted explanations were, well, a little ambiguous and vague, is a bit of an understatement. It would not be too harsh a judgement to say they were just flat out wrong.
Fortunately, in his continuing quest for knowledge the author of CooperToons just happens to have studied the branch of chemistry that has the power to resolve what we can call the "Problem with Pyrene" (sounds like an old Gidget movie, doesn't it?). So for those who can't sleep at night worrying why a compound with 4n electrons acts like those with 4n + 2, read on!
Background of a Conundrum: Dot's, Stability, and Erich.
All those unfortunates who have had to take organic chemistry will have been bombarded with a milliard of notations. symbols, and rules. You'll read about reactions that are SN1, SN2, E1, and E2 and use symbols like δ-, δ+,
But without doubt, among the most famous of the rules has to be the one we just mentioned, the 4n + 2 rule, or perhaps better known amongst chemists as Hückel's Rule.
Hückel's Rule was developed by the German physicist Erich Hückel - yes, Erich was a physicist, not a chemist. His purpose was to explain the properties of what chemists call aromatic compounds. Originally aromatic compounds were classified as compounds that 1) have a particularly pungent aroma, and 2) were "unsaturated".
Now "saturated" and "unsaturated" are words familiar to the modern consumer when referring to fats and oils. The actual chemical meaning, though, is that that an unsaturated compound has less hydrogen atoms than the corresponding saturated molecule. For instance, one component of saturated fats (sounds like the name of a pool hustler, doesn't it?) is stearic acid, C18H36O2. A corresponding unsaturated acid is linolenic acid, C18H30O2, with six fewer hydrogens.
It was later found that aromatic compounds are cyclic. That is the carbon atoms in the molecules formed rings. This helped explain why aromatic compounds are even more unsaturated than the typical unsaturated compounds. As we see below, making a ring means you loose two hydrogen atoms from the corresponding "linear polyene". This was first recognized by the French chemist, Auguste Kekulé, who said the idea came to him while he was dozing off.
Linear Polyenes and Cyclic Aromatics
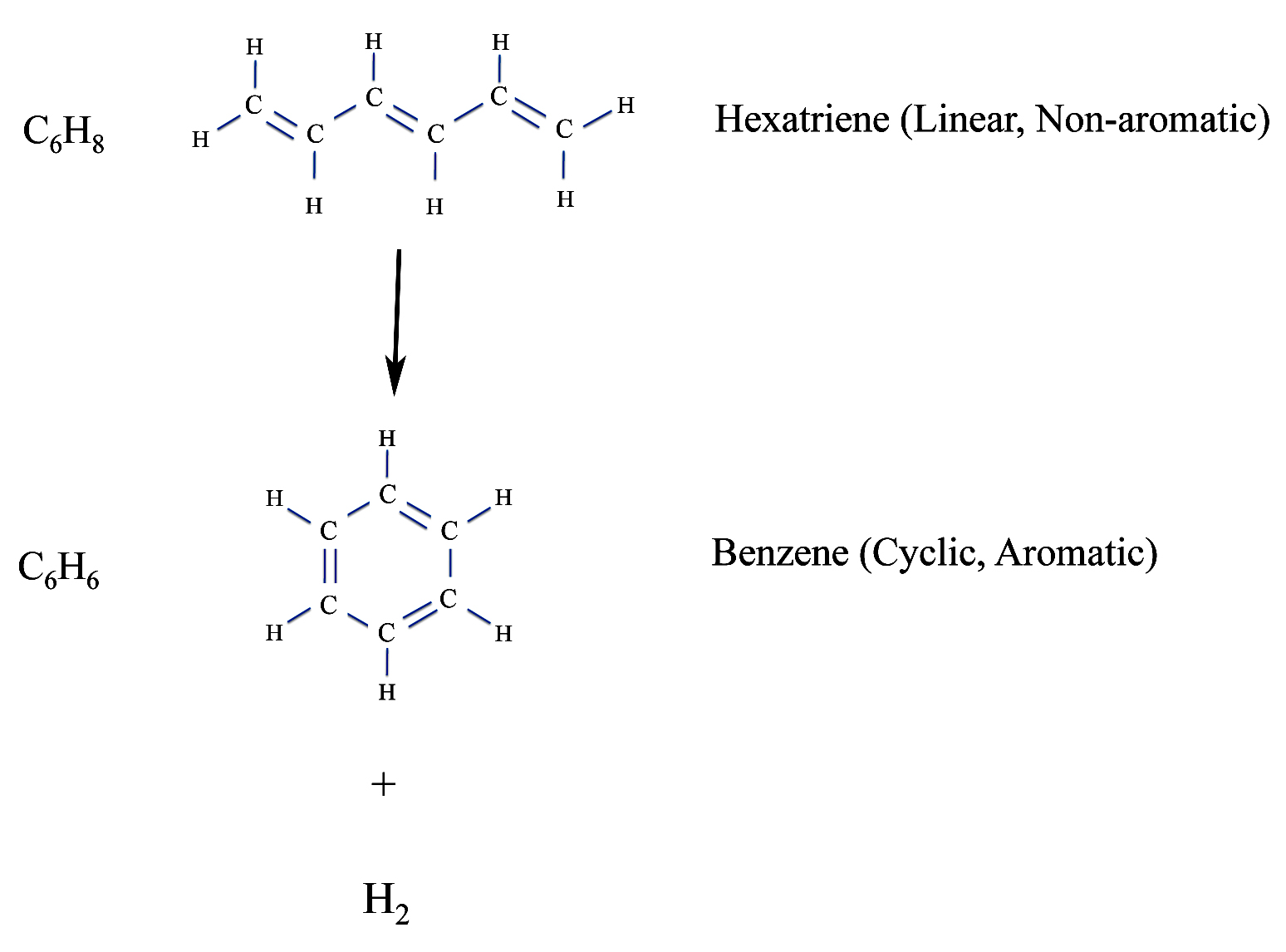
But what chemists found to be the most interesting property of aromatic compounds was their extra stability. Now the use of the word "stability" - although common - is somewhat unfortunate. It can mean different things. Strictly speaking a stable molecule is one that won't spontaneously fly apart into it's individual atoms. For instance, O2, oxygen gas, is a stable molecule. However, Ne2 is not. For that reason it doesn't exit.
But when chemists say a molecule is not stable, they usually mean it has high reactivity. For instance, if you add a molecule of bromine - Br2 - to hexatriene - our non-aromatic compound shown above - you form dibromohexadiene. But if you add bromine to benzene, nothing happens except the bromine dissolves. Benzene is not reactive in this case and so we say it has high stability.
Erich was trying to explain this unusual stability - we'll keep using the term - of benzene. But before we proceed with what Erich did, we'll pause for those whose chemistry is, if not rudimentary, then a bit rusty. This will also let us set up the basics for understanding the chemistry of pyrene.
Chemical Basics: A Brief Review
Now one thing that made chemists and physicists realize there was something special about benzene is that when you try to draw it using the "classical" formulas, you run into problems.
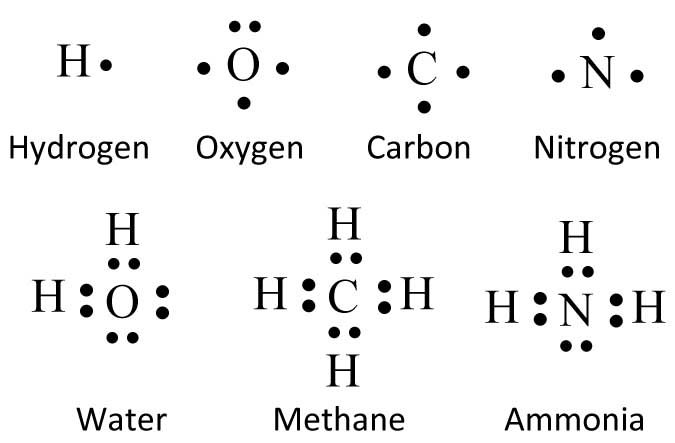
The way we draw chemical structures is based on the "electron dot" diagrams devised by Gilbert Newton Lewis around 1916. Atoms are represented by letters with the appropriate number of dots around them. As anyone who has taken middle school chemistry knows, electrons in atoms occupy inner and outer "shells" surrounding the nucleus, sort of like planets circling the sun. Usually only the outer electrons form the chemical bonds. These are the "valence" electrons. You only need to draw the valence electrons in a Lewis diagram.
Now for many chemical compounds - especially carbon compounds - the atoms obey the "octet" rule. That is the outer shell of the atom likes to have eight electrons. The electrons can be shared with other atoms including hydrogen. Hydrogen, though, can only have a maximum of two electrons.
Lewis - "Electron Dot" - Diagrams: Atoms and Molecules
The sharing of electrons makes the type of chemical bond called a covalent bond. When only two electrons are shared between atoms you have a single bond. Sharing four electrons gives you a double bond and six shared electrons gives you a triple bond.
Single, Double and Triple Bonds

Since having all those dots gets unwieldy we usually represent pairs of electrons as a line between the atoms. When you do this benzene has the familiar hexagon shape with a ring made up of carbon atoms bound with alternating single and double bonds. For even greater and more admirable brevity, we don't even need to use the letters. Just draw the lines and you understand that the carbon atoms are where the lines meet. The number of hydrogens is equal to 4 minus the number of lines attached to the carbon. Simple enough.
Benzene (C6H6) - Dots and Lines and Admirable Brevity

Now at this point we need to clarify just what the actual 3D molecule looks like.
Benzene (C6H6) - The Sigma Bonds
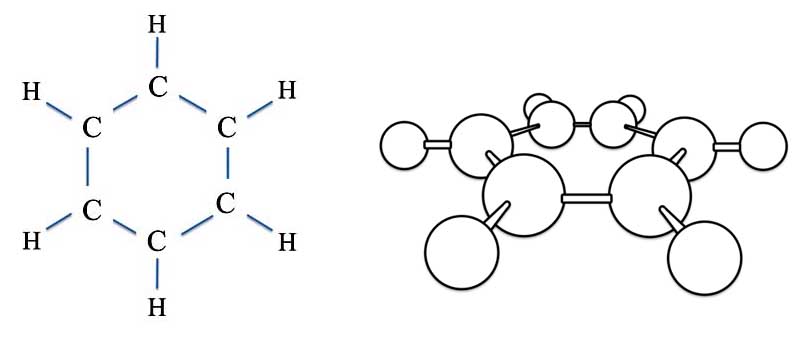
All the atoms of benzene lie in a single plane. The basic "skeleton" - the sticks in the drawing above - represent two electrons between the atoms. These type of bonds are called the sigma (σ) bonds. The view on the right is of the molecule laying more or less on its back.
Double bonds are formed when you have a combination of the sigma bonds - the sticks between the carbons - plus electrons in dumbbell shaped orbitals called p-orbitals. The p-orbitals are oriented perpendicular to the plane of the molecule. The p-electrons form what are called pi bonds (π) and the electrons of a pi-bond congregate above and below the plane of the sigma bonds.
The simplest example of making a double bond from a sigma and pi-bond is from ethylene, which is a chemical that makes fruit ripen.
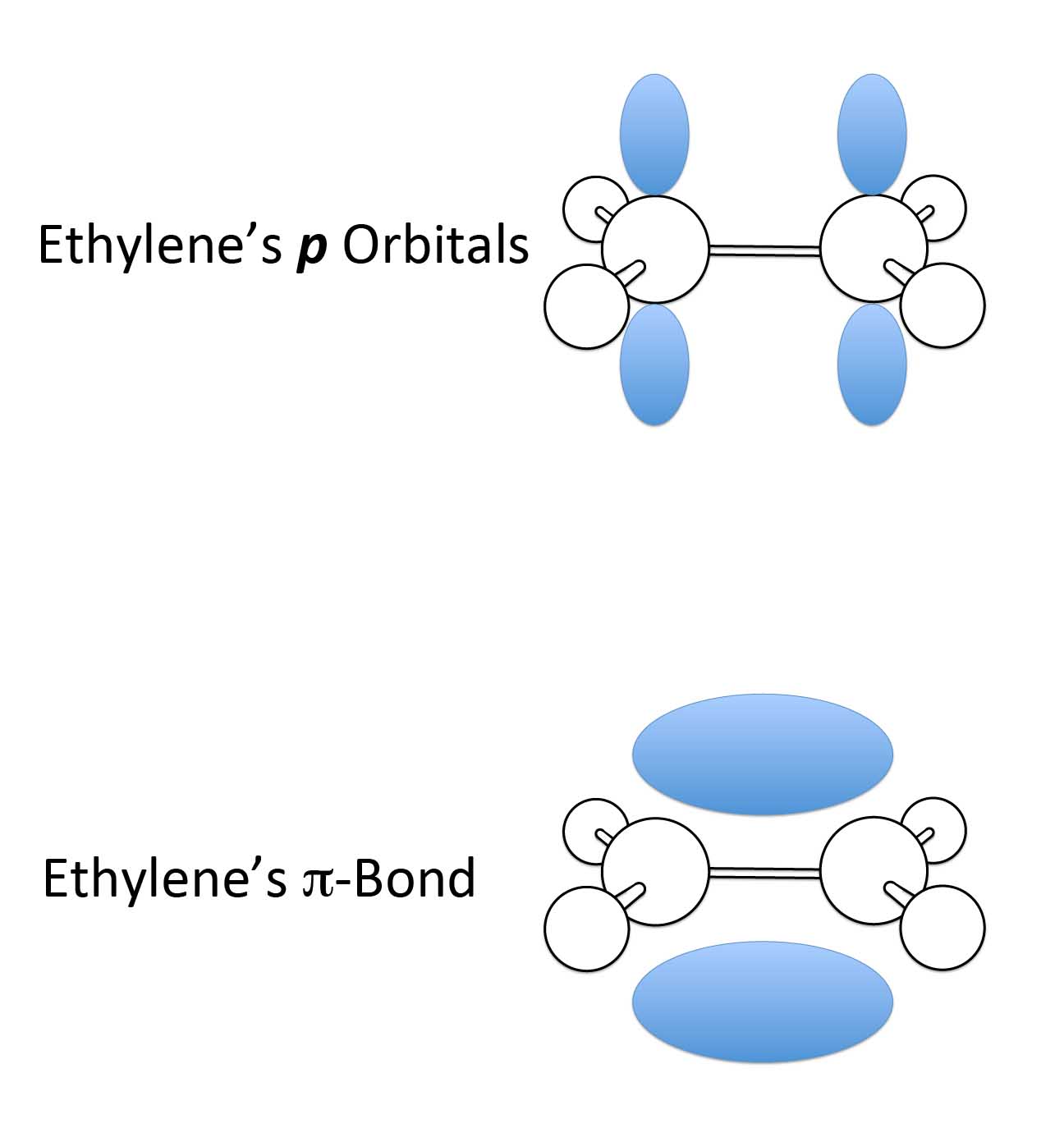
The two p-orbitals overlap above and below the sigma bond. The sigma and pi-bond combination is what gives us our double bond.
For benzene, though, we have six p-orbitals.
Benzene (C6H6) - The Sigma and Pi Bonds
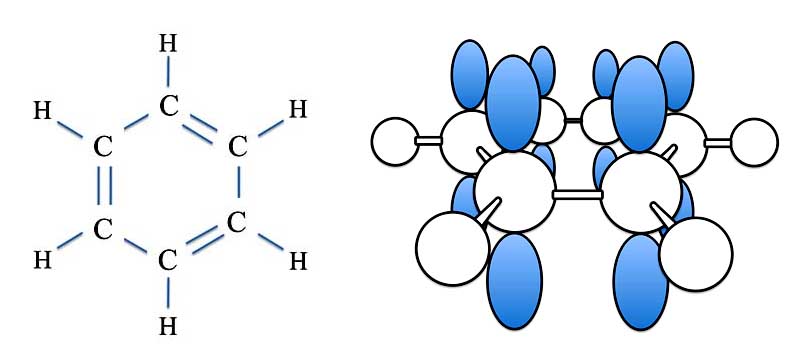
You can see the problem. Which p-orbitals overlap with which to form an actual double bond?
Another way to look at the problem is to try drawing the benzene molecule with double and single bonds. If you keep track of the carbon atoms - that is, label each one with a number - then you can draw the double bonds in different places. The double bonds - with eight electrons - can link atoms 1 and 2, atoms 3 and 4, and atoms 5 and 6. Or you can draw them from atoms 2 and 3, atoms 4 and 5, and atoms 6 and 1.
Now this is usually explained as saying benzene is not either of the individual structures. Instead the real benzene is a resonance hybrid of the two. So you really have the electrons delocalized over the whole ring and you have six one-and-a-half bonds instead of three double and three single bonds. A common way to draw benzene in modern textbooks is to use a circle - either dotted or solid - in place of the double bonds.
Benzene (C4H6) - Resonance Structures
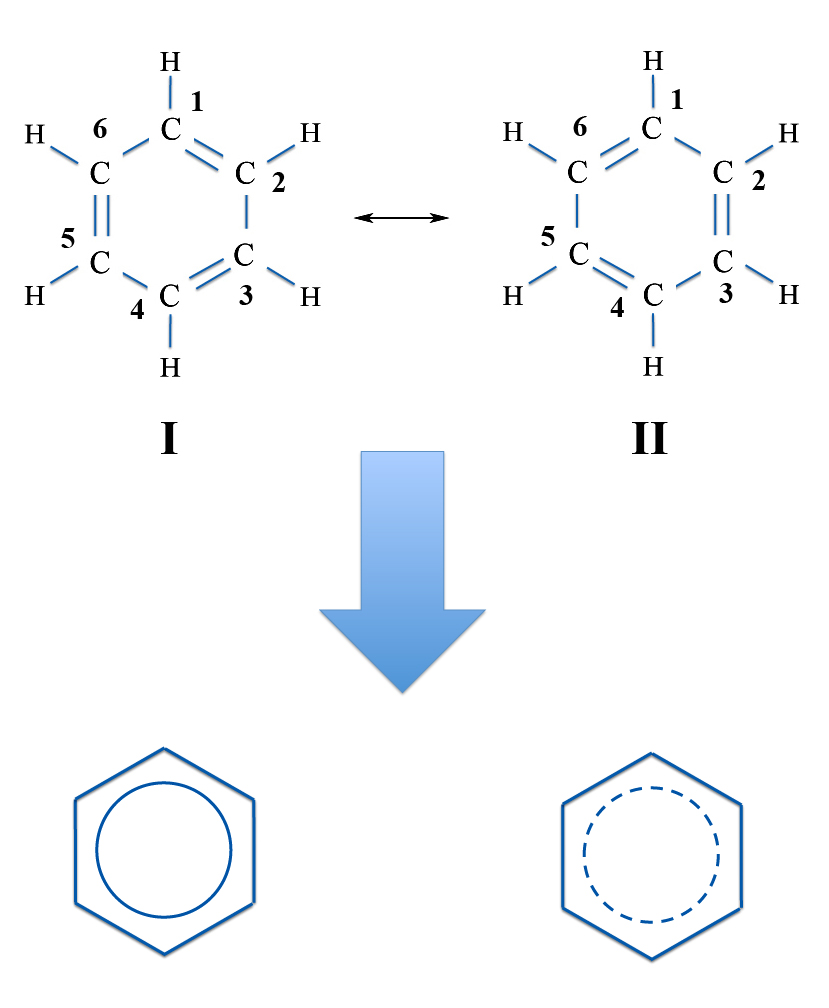
And "Modern" Pictures
Because the two resonance structures are identical, both are equally important. Also note that the two individual structures obey the classical rules of drawing the structures. The bonds connect nearest neighbors and all carbon atoms have four bonds.
Now consider molecules that aren't in a ring such as butadiene (used in making rubber). Note that you can't draw more than one classical formula. You really have to keep the double and single bonds where they are unless you draw really oddball structures.
Butadiene (C4H6) - Resonance Structures
So as Flakey Foot asked Mr. Natural, "What does it all mean?" Well, the first explanation was that compounds with multiple resonance structures like benzene - where each structure has the "classical" double and single bonds - have greater stability due to the electrons being spread out over the actual ring. The more "classical" structures - but avoiding oddball ones - the more stable the molecule and the less it reacts like compounds with ordinary double bonds.
But sadly that rationale doesn't work. Consider the molecule below. This is cyclobutadiene. It also has two "classical" structures, just as does benzene. But cyclobutadiene isn't stable. You can't even make it unless you're at 8 degrees Kelvin - that's -265 degrees Celsius or a frigid -445 degrees Farhenheit. It completely vanishes at 35 degrees Kelvin when it begins to react with itself.
Cyclobutadiene (C4H4)
Resonance, Si! Stability, No!
So what, we ask, is going on?
Enter Erich
We can now return to Hükel's Rule. We won't go a great deal into how Erich did his actual calculations (although you can download a spreadsheet to do your own Hückel calculations if you click here - but be sure to enable the macros). However, the mathematics of Hückel calculations don't involve anything more than solving simultaneous equations of the type you learned in middle school math. Without computers the calculations were a bit tedious, true, but they could be done.
Erich Armand Arthur Joseph Hückel was born in 1896 - one year before Moe Howard of the Three Stooges - and received his Ph. D. at the University of Göttingen. He originally worked with the theory of electrolytes (developing the Debeye-Hückel theory that even today torments students of physical chemistry). Then around 1930 he began to explore a form of quantum mechanics called molecular orbital theory.
There are two basic approaches to using quantum mechanics for molecules. Both represent the molecule as a complex mathematical equation. But the methods differ in how you construct the equation.
One approach is the valence bond or VB method. Valence bond theory treats the electrons as if they are localized between pairs of atoms. Naturally this approach had an early appeal to chemists. For compounds like benzene, though, you have to take the formulas that correspond to the individual resonance structures and combine them to get the best equation for the entire molecule. The VB approach was particularly favored by the American chemist, Linus Pauling, today best known for his enthusiastic advocating of large doses of Vitamin C for curing diseases and maintaining good health.
In molecular orbital or MO theory, though, there are no specific bonds per-se. Instead the electrons are allowed to spread over the whole molecule. Although this seems to go against the idea of a chemical bond, you can show that in many cases the electrons do congregate between the atoms forming a more or less classical picture of chemical bonds.
However, the electrons in a molecule - as in atoms - can have only discrete energy values. The electrons of a particular energy also have some restrictions on where they can be in space. A particular regions in space which corresponds to a specific energy level is called a molecular orbital. Hence the name of the theory.
Erich's theory was that the unsaturated molecules - ethylene, butadiene, hexatriene, benzene, or whatever - can be understood by using only the few electrons in the p-orbitals. The other electrons that form the sigma bonds don't enter into the actual calculations.
Although you can give the energy levels of the orbitals in some absolute numbers like BTU's, joules, calories, or electron volts, Erich found it more convenient just to use relative values in what he called beta units (β). For an isolated atom - that is, an isolated p orbital, the energy is set at zero β units.
Erich realized the simplest place to start was with ethylene. We've already seen that ethylene has two carbon atoms and each carbon atom of ethylene has one p-orbital that contributes to the double bond. Since each p-orbital has one electron our calculations concern only two electrons.

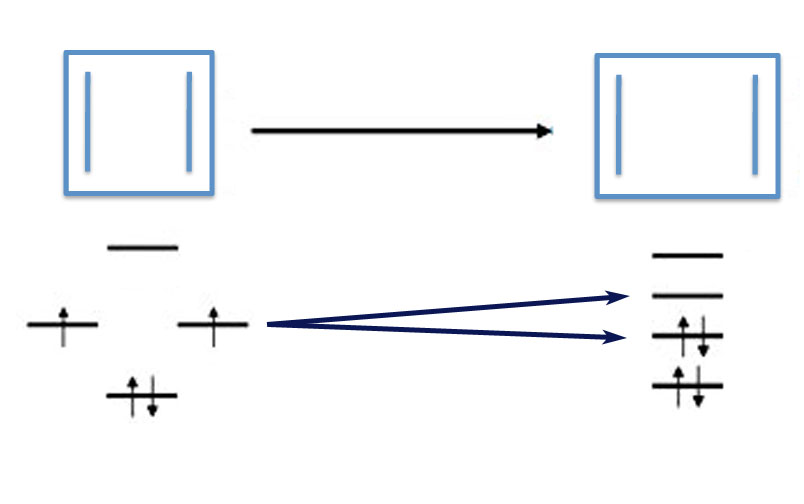
A characteristic of molecular orbital theory is that you end up with the same number of molecular orbitals as atomic orbitals. So with 2 p orbitals - one from each carbon atom - you get two molecular orbitals and two energy levels. In ethylene the energy levels - using the β units Erich devised - are -β and +β.
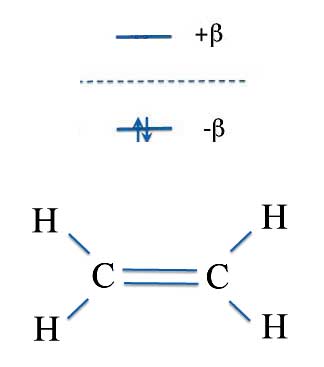
If you'll remember your chemistry, it is possible to put two electrons - but no more - into any orbital (molecular or atomic). And they fill the lowest energy levels first. So for ethylene the two p-electrons both reside in the lower energy orbital. This filled orbital makes the chemical bond. In general the electrons in energy levels with a negative sign indicates the electrons are creating chemical bonds and are called the bonding-orbitals.
Because there are now two electrons in the bonding orbital, the total energy of ethylene's pi-bond is twice the energy of the orbital.
Total π-Energy = 2 Electrons × β = 2β
The higher level orbital at +β has no electrons. Energy levels with positive β values are called the anti-bonding orbitals. For our purposes we don't need to worry about anti-bonding orbitals.
[Note: The sharp eyed readers will notice that although the more stable energy levels have negative numbers, the total energy - also called the binding energy - is given as a positive number. Although this is a bit inconsistent, this is the usual convention.]
After he ran the calculations on benzene and cyclobutadiene Erich found that cyclobutadiene and benzene have similarities but also important differences. Both have their lowest energy level at -2β and the next two energy levels have equal energies. Energy levels with equal energies are called degenerate levels.
Benzene and CycloButadiene
Hückel Energy Levels
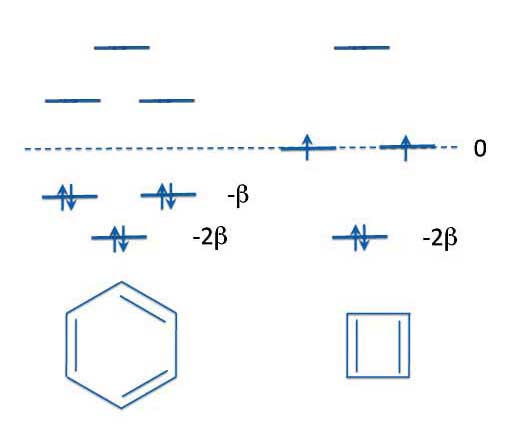
Now in benzene these next two energy levels are at -β - that is, they are bonding orbitals. But in cyclobutadiene the next two degenerate levels are at 0β. That is, they have the same energy as isolated p-orbitals. So they don't contribute anything to the bonding of the molecule. Orbitals with a zero beta energy are therefore called non-bonding orbitals.
But the really important thing to notice about cyclobutadiene is that we've run out of electrons if we want to fill both of the non-bonding orbitals. Just which of the two degenerate orbitals do the electrons go into?
The rule is that one electron goes into one orbital and the other in the other. Why? Well you can think of it in terms of simple electronic repulsion. If both electrons occupy the same orbital you have two negatively charged particles competing for the same space. But if they are in different orbitals it's easier for them to stay apart. Hence, two electrons in two orbitals is a more stable situation.
But two unpaired electrons form what is called a di-radical (a molecule with a single unpaired electron is just a radical). Radicals are usually reactive molecules and are not stable. So cyclobutadiene not only has higher energy electrons than benzene, but the electrons are unpaired and so the molecule is highly reactive.
On the other hand, benzene's six orbitals can fill in all the lowest energy levels which have negative energies. And all electrons are paired. Hence, benzene is a stable, non-reactive molecule.
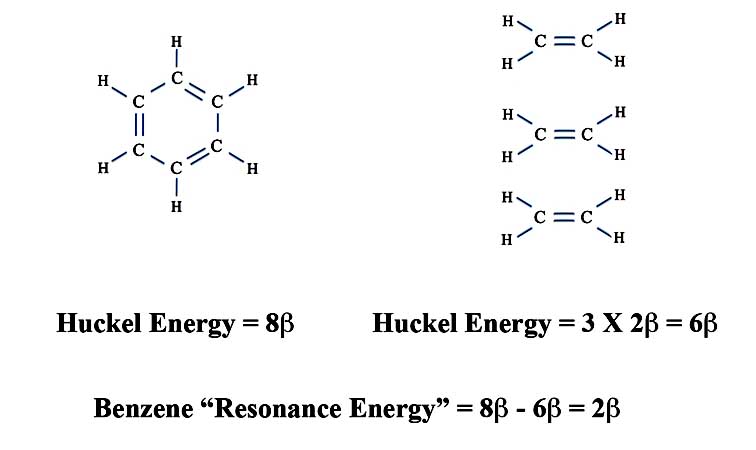
Erich also pointed out that since benzene's classical structure has three double bonds and three single bonds, we can calculate the difference in the total pi-energy of benzene compared to that of three isolated double bonds. We know the energy of one double bond from our ethylene calculation is 2β. The total pi-energy of benzne is:
| Energy of Benzene (β) | = | 2 × 2β + 2 × 1β + 2 × 1β |
| = | 8β |
So now we can determine the extra energy when the electrons spread out over the benzene ring. This delocalization energy of benzene is also called the resonance energy and is:
Resonance Energy of Benzene as Erich Calculated
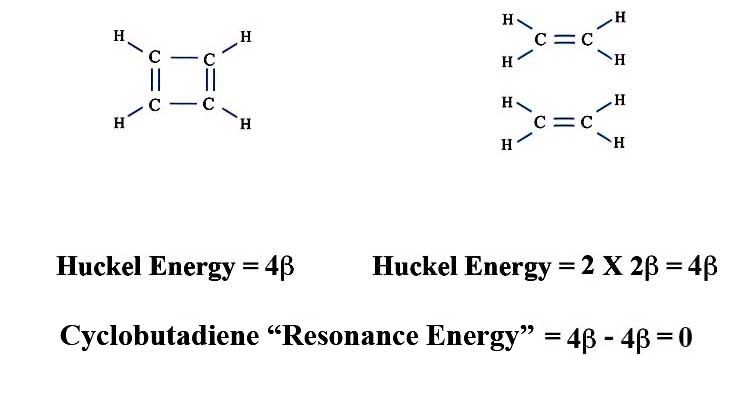
Apply the same calculations to cyclobutadiene and you get:
So we can sum up Erich's molecular orbital theory - Huckel Molecular Orbital or HMO Theory - as to how it explains why benzene is aromatic and stable and cyclobutadiene is not stable and not aromatic. Cyclobutadiene has reactive electrons at high energy but there is no resonance energy to help stabilize the molecule. But benzene has it's electrons nicely paired up in low energy levels. Benzene also has a positive resonance energy which gives it more stability than expected from the classical structure.
(As an aside we should point out that as with total or binding energy, when we talk about resonance energies, more stability is indicated using a positive number.)
Eric didn't stop at benzene and cyclobutadiene. He also extended his calculations to rings with more carbons. Such ring structures with alternating double and single bonds are called annulenes.
Erich's calculations showed us that as long as the rings are planar, rings with 4, 8, 10, 12, 14, 16, and on up are reactive di-radicals. If you have 6, 10, 14, 18 or 4n + 2 electrons you have nice paired electrons.
This then is where we get the famous Hückel's Rule or the 4n + 2 Rule. Cyclic molecules with 4n + 2 electrons are aromatic and stable, those with 4n electrons are di-radicals and not stable.
Case closed, nicht wahr?
Weeeeelllllllll, not quite.
The Real Hückel's Rule
Now at first glance Hückel's Rule seems to hold up well. After all, look at naphthalene, anthracene, and phenanthrene. Naphthalene (moth balls) has 10 electrons and anthracene and phenanthrene both have 14. All have 4n + 2 electrons and yes, they are aromatic compounds.
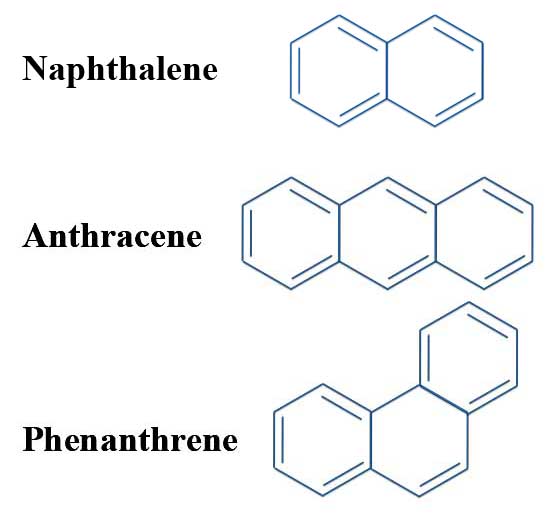
But now look at this molecule. This is our friend pyrene. It has a total of 16 π electrons. That is, 4n electrons.
Pyrene: A 4n Aromatic Compound
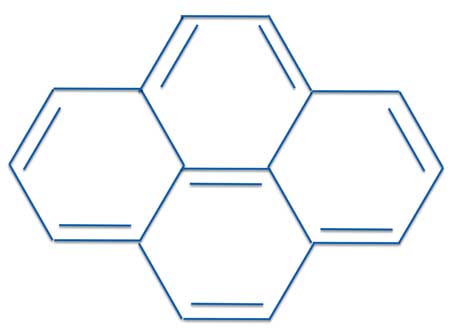
Well, according to Erich's 4n + 2 vs. 4n electron rules, pyrene should not be stable.
But that's not what experiment tells us.
Pyrene is in fact a perfectly stable compound.
Not only that, it is aromatic.
We repeat, by all experimental and physical criteria, pyrene is an aromatic compound that does not obey Hückel's Rule.
So how can we explain the Problem with Pyrene?
Well, one textbook tries to explain the pyrene contradiction as saying you should ignore the "internal" bonds in aromatic compounds with more than one ring. So ignore the bond in the middle of pyrene, and you'll have 14 electrons or a nice 4n + 2 number where n = 7.
Pyrene: Center Bond?
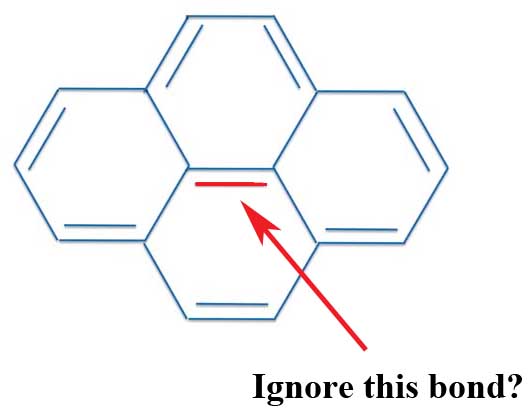
Now this type of explanation is politely called hand-waving or what eggheads call not only an ad-hoc argument but even post-hoc. That is, you have a rule that doesn't work, but after the fact, you wave your hands and try to explain that your theory really is right even though it is clearly wrong.
Unfortunately, you run into a problem with the "ignore-the-middle-bond" argument. After all, you can draw pyrene as a perfectly acceptable alternative resonance structure.
Pyrene: Resonance Structure II
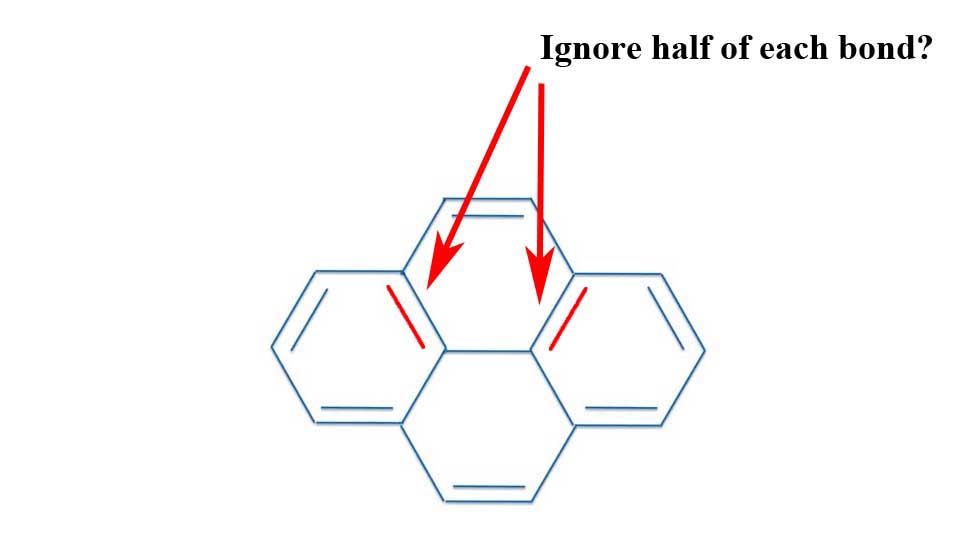
Are the two bonds that stick toward the center "internal" bonds? If so, you should ignore them and you have 12 electrons - yes, 4n. If you don't ignore them you have 16 electrons - the original 4n. But since the bonds are only sort-of-internal perhaps we should just ignore half of their electrons. That would give us 14 electrons - 4n + 2. But this explanation is about as hand waving, ad hoc, and post-hoc as you can get. It isn't really an answer.
Michael Steps In
To explain the Problem with Pyrene, now we need to introduce a rather interesting character. That was Professor Michael J. S. Dewar.
Michael James Steuart Dewar (the "Steuart" is the correct spelling, not a misprint) was born in 1918 in India of British parents. His dad was a civil servant, but died when Michael was still a boy. So Michael and his mom returned to England, and Michael attended a boarding school. After graduating he attended Balliol College at Oxford where he studied - "read" to use the British patois - chemistry.
Balliol was one of the oldest colleges at Oxford - stretching back before Chaucer - and it was one of the most prestigious. Traditionally it had catered to the scions of the posh families and also included a healthy percentage of students from the colonies. Of course, by Michael's time at university (for some reason the British like to leave out "the"), there were more Oxonian colleges to choose from. Some had become amendable to the middle or even working class students. One joke was that if you walked into the quadrangle of Jesus College and shouted "Jones!" every window would fly open.
Like most chemists at that time Michael worked in the lab. Chemistry, by the Great Liebig, was an experimental science, happily uncontaminated with mathematical brouhaha as you had in (ptui) physics. After all, everyone knew that mathematics in chemistry was not only unnecessary but actually detrimental. Or as as Auguste Comte put:
Any attempt to employ mathematical methods in the study of chemical questions must be considered profoundly irrational and contrary to the Spirit of Chemistry.
If Mathematical Analysis should ever hold a prominent place in chemistry - an aberration which is happily almost impossible - it would occasion a rapid and widespread degeneration of that science."
This attiude, by the way, persisted well into the computer age. One Nobel Prize winning chemist would refuse to sign a theoretical doctoral thesis unless the candidate had done some experimental work as well.
For Michael's part, once he got his undergraduate degree, he stayed at Oxford and got a masters degree, and then in 1942, his Ph. D. He then began post-doctoral studies with the legendary Sir Robert Robinson.
By the time Michael reached Oxford, Sir Robert was probably the best known of the synthetic organic chemists - that is, chemists who specialized in preparing carbon compounds. His forte was isolating, preparing, and studying natural products, and he particularly liked working with compounds from the Brazilwood tree. Brazilwood is not only great for making violin bows, but it also contains a number of compounds which have enough complexity to make them interesting, but also have enough simplicity for chemists working in the pre-instrumental days to analyze. Besides, Sir Robert said, the compounds were so colorful that just working with them was its own reward.
It was during the course of his work on natural products that Robert had become interested in chemical theory and it was partly due to Sir Robert's interest - and that of his colleagues - that theoretical chemistry made real strides. In 1900 people were still debating whether atoms really existed (Einstein showed they did in 1905). But by 1920, the atomic and molecular theory had assumed its more or less correct form. There was, though, relatively little mathematics involved and chemical theory was mainly drawing structures and showing where the electrons moved around going from reactants to products.
Sir Robert always believed he was the true inventor of the modern "classical" theory of organic chemistry, a belief that led him into a bit of a dispute - to put it mildly - with Sir Christopher Ingold who also had a claim to being the Father of Modern Organic Chemistry Theory. You can read about this rather epic battle of the minds if you click here. But for now, we'll let it pass.

Sir Robert and Sir Christopher
Somewhat at odds.
Michael tells us that Sir Robert never thought much of resonance theory. It was nothing more than what he had already been doing. But he also had a strong distrust of quantum theory. Erich's apparent success with explaining aromatic compounds didn't impress him. There were in fact some pretty severe problems with Erich's theory, not the least that it really didn't explain aromaticity at all!
Earlier we mentioned Erich's definition of benzene's resonance energy. That's the difference between between the real energy of benzene and three isolated double bonds. We showed that benzene's π energy is 8β and a double bond is 2β. So benzene's resonance energy according to Erich is 8β - 3 × 2β = 2β.
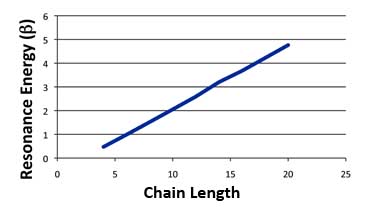
There's a problem with this definition. For instance take the annulenes - the molecules with alternating single and double bonds in a ring. The smallest member is our friend cyclobutadiene and the next one is benzene. We've seen that cyclobutadiene's resonance energy is zero, and benzene's is 2β.
But then start calculating the resonance energies for larger and larger rings: 8, 10, 12, 14, and on up. Calculate the resonance energy by Erich's definition, you get a graph like:
Hückel Resonance Energies for Annulenes

In other words, everything from benzene on up has a large resonance energy!
So instead it looks like we have to rely on the di-radical nature of the 4n annulenes to explain their reactivity. But there's a problem with that explanation, too. If you go to a bit more rigorous calculations, it turns out that single unpaired electrons in orbitals of equal energy will combine to form a lower energy orbital which holds both electrons and a higher energy orbital which doesn't hold any electrons. This Jahn-Teller Effect not only distorts the molecules a bit, but also invalidates the argument that 4n annulenes are di-radicals.
The Jahn-Teller Effect
No Di-Radicals for 4n Rings
But worse is to come. If we stick with Erich's definition of resonance energy then even non-aromatic compounds have resonance energy, for crying out loud! Look at straight chain polyenes - that is, alternating single and double bonds but not in a ring. According to Erich's definition, these also have positive resonance energies. And they're not radicals either!
Hückel Resonance Energies for Polyenes
So after all that work, it looks like Hückel Theory doesn't explain anything after all.
Although Michael agreed with Sir Robert that resonance theory was simply the classical theory in disguise, he disagreed that quantum mechanics had no potential for the chemists. If the mathematics could be worked out, he saw it could be an intriguing new tool. And he was in a good place to set things right.
By the late 1940's Michael had become the Professor of Chemistry (equivalent to department chairman in the US) at Queen Mary College at the University of London. This brought him into contact with chemists, physicists, and mathematicians at the U of L who were working on quantum mechanics. One physicist who would later be professor of mathematics and chemistry at Oxford was Charles Coulson.
First Michael had to set the record straight on what he thought about resonance theory. So in 1949, Charles and Michael published a paper where they said there was no real connection between valence bond wavefunctions of quantum mechanics and resonance structures. Instead, they pointed out, there were some characteristics from molecular orbital theory - the type of calculations that Erich used - that could explain the apparent successes of resonance theory.
At this point we should mention that at higher and higher levels of rigor, molecular orbital theory and valence bond theory move closer and closer to giving the same answers. Charles said that MO and VB theories are almost equally valid, and Michael, too, said that valence bond theory is a perfectly valid way to create wave functions. Their quibble wasn't with VB theory.
But there's no doubt about one thing. Michael never bought onto resonance theory. He felt that its connection to valence bond theory was entirely specious. But the real problem with resonance theory was it was simply too vague and had few real rules. To quote Michael, "It can be played happily by almost anyone without any knowledge of the underlying principles involved."
For advocates of resonance theory, though, Michael's objections certainly seem rather strange. For one thing he always maintained that resonance theory was equivalent to the classical theory of Sir Robert. And yet he praised Sir Robert's contribution to chemical theory. How can you praise one theory and trash another that is equivalent? And he and Charles said resonance theory is not based in quantum mechanics. But on the other hand, they used quantum mechanics - MO theory - to explain why resonance theory gives correct answers.
But hold on there! Doesn't that mean resonance theory works?
Michael stuck to his guns. Resonance theory was simply a reformulating of the classical theory of Sir Robert - and it was worse. It is not only ad hoc but post hoc, and had really done nothing for advancing chemical theory.
The PMO Method: A Perturbing Theory
Now we can return to the Problem of Pyrene.
But one more thing ...
Michael was not a man to simply whine and criticize (we have chatrooms for that). If he saw something was wrong, then he would come up with a proper solution. Certainly if organic chemists should drop resonance theory for something really based in quantum mechanics, he would have to provide it. And it needed to 1) work better than resonance theory, and 2) be just as easy.
In 1952 Michael was a visiting professor at the University of Notre Dame. There he wrote up a series of papers that were published in the Journal of the American Chemical Society. These were titled "A Molecular Orbital Theory of Organic Chemistry", and they explained how simple Hückel calculations together with a quantum mechanical technique called perturbation theory could explain the complex behavior of conjugated organic compounds - whether aromatic or not.
Although the rules are derived from horrible looking equations, the actual application of what Michael called the Perturbational Molecular Orbital (or the PMO) method required the simplest "back-of-the-envelope" calculations. So we'll skip the theory and just dive into how we determine if a compound like benzene is aromatic or not.
First take your conjugated π-compound which has an even number of carbon atoms. Then divide it into two parts with odd numbers of atoms. For instance with benzene you can divide it into two parts of three atoms each.
Perturbation Theory: Dividing Benzene
Now we will not be drawing any resonance structures. That means we do not need to draw specific single or double bonds. We will even ignore any indications of the electrons at all!
Next, you mark each atom with either an asterisk (*) or a zero (0). But you have to follow the following rules:
- There must be more *'s than 0's.
- No * must be next to another * and no 0 can be next to another 0.
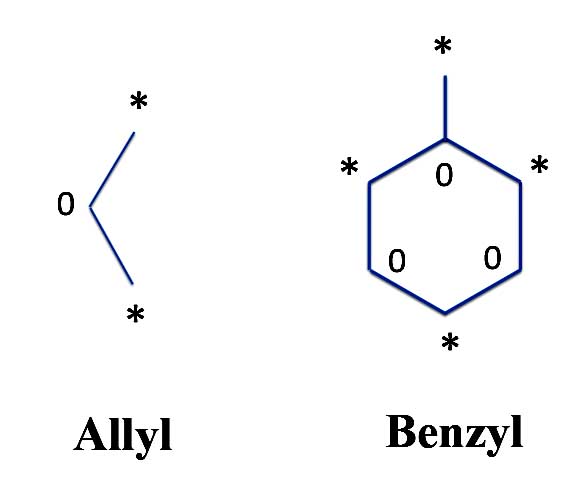
For instance, consider the three atoms of our benzene half which we will called an allyl radical (since odd numbered "molecules" have an odd number of electrons, they are radicals). It has two *'s and one 0 in the middle. Another slightly more complex example is the benzyl radical where one of the 0's is surrounded by three *'s:
Asterisking Allyl and Benzyl Radicals
At this point we assign a number to the asterisks. You can start of with any number but low integers are best. But again there are rules.
- The numbers can be positive or negative.
- The sum of all numbers surrounding a zero must add up to zero.
For our allyl and benzyl radicals one way of numbering them is:
Numbering Allyl and Benzyl Radicals

Now there is nothing sancrosanct about using 1's and 2's. We could have started off using any number. That's because we will now normalize the numbers. We do that by:
- Squaring each number.
- Adding up the squares.
- Taking the square root of the reciprocal of the sum to give us the normalization constant.
- Multiplying the original number by the normalization constant.
This is illustrated by:
Allyl and Benzyl: Numbered and Normalized
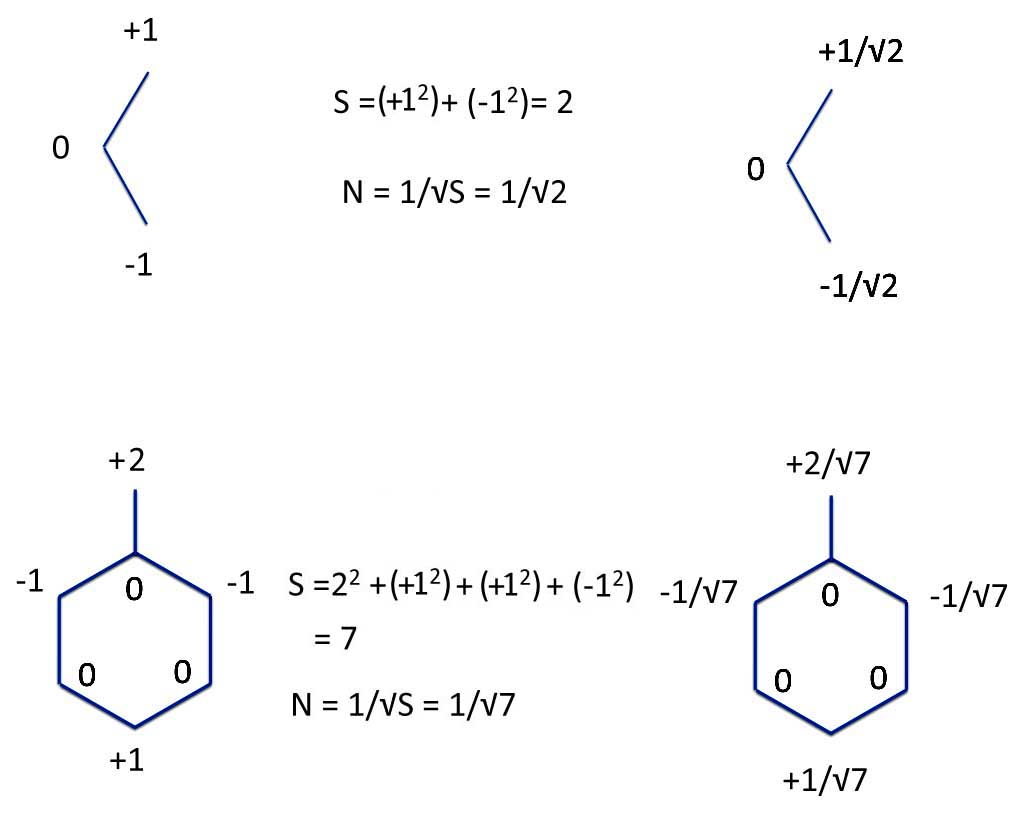
What Michael's PMO method did was to allow you to calculate the energy (in Erick's β units) if you bring the radicals together. You do this by multiplying the coefficients of the atoms that are forming the bonds. But you want to make sure that you have as many like-signs as possible. That is you match the positive and negative coefficients as well as you can. Then you add everything up.
For instance, if you bring the allyl radicals back together, you end up (obviously) with benzene.
2 Allyl -> Benzene
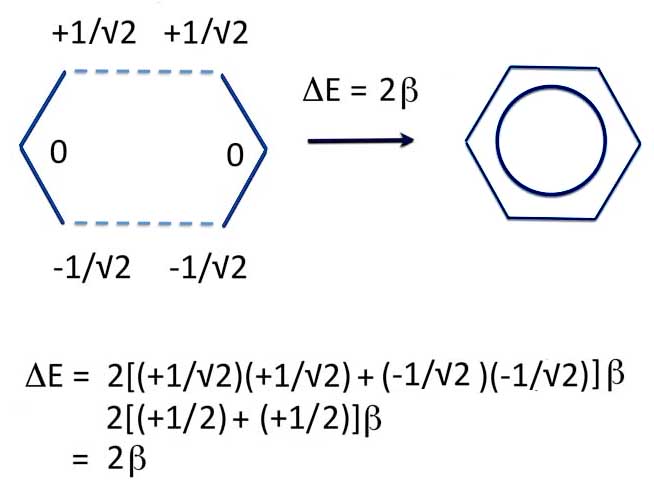
So when you make benzene from two allyl radicals, the energy is 2β units lower. That is, benzene is more stable than the radicals.
Michael referred to two radicals of a PMO calculations as an R-S pair. The two don't need to be the same - they usually aren't - and the only requirement is only they have odd numbers of carbon atoms. So the smallest number of carbons of a PMO radical is 1 - a single carbon atom (called a methyl group). The number associated with the methyl group is +1 (or in some cases -1).
For instance, you can make benzene by bringing together the "methyl" group with a five carbon radical, the pentadienyl radical.
R-S Pairing
Pentadienyl + Methyl → Benzene
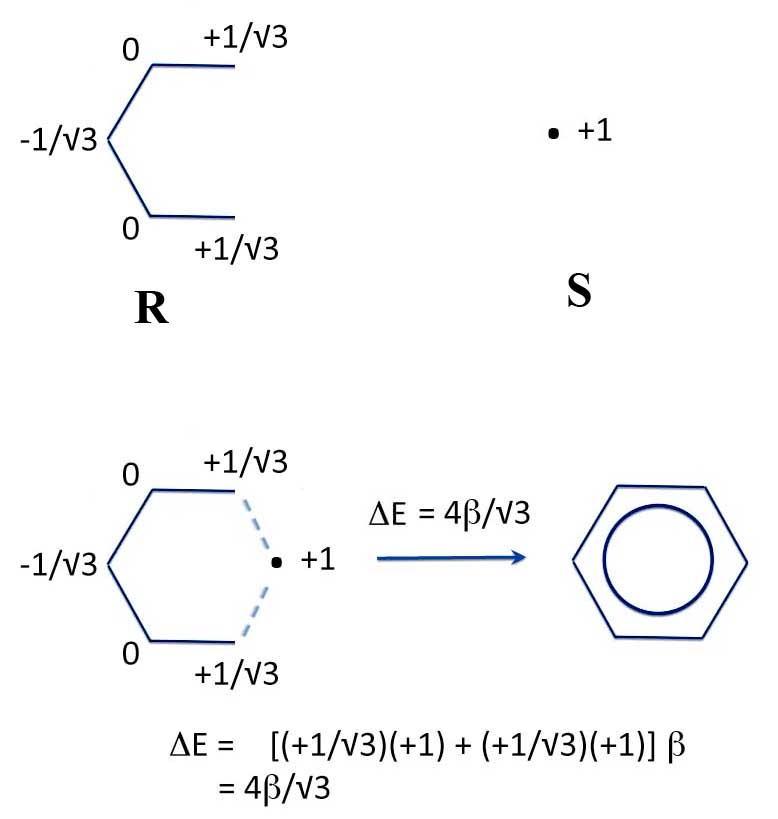
Admittedly we don't get exactly the same energy change as when we used two allyl groups. That's understandable since the pentadienyl/methyl radical R-S pair doesn't have the same energies as two allyl radicals. Also you can point out that the PMO method and Hückel theory are approximate methods and so you should expect minor discrepancies. Both of these explanations are, in fact, correct.
But what, we ask, is the point? We can take benzene apart and put it back together? And we can calculate the energy when we do it? But how does that help us understand pyrene?
Because the PMO method gives us a way to calculate resonance energies. But a bit differently than Erich.
Resonance Redefined (à la Michael)
Here Michael stepped in and made a real change. He reasoned that using isolated double bonds as the reference structure is artificial and inconsistent with chemists' real definition of aromaticity. We define aromatic compounds - compounds in a ring - because they are different from compounds with the same number of double bonds that are not in a ring. We don't define benzene as aromatic because it is different from three ethylene molecules, but because it is different from hexatriene - three double bonds in a straight chained molecule.
The reference structure therefore should be the corresponding straight chain. Or in other words, we ask if a molecule acquires stability when it goes from a straight chain polyene to a cyclic annulene.
Michael's Reference Structures:
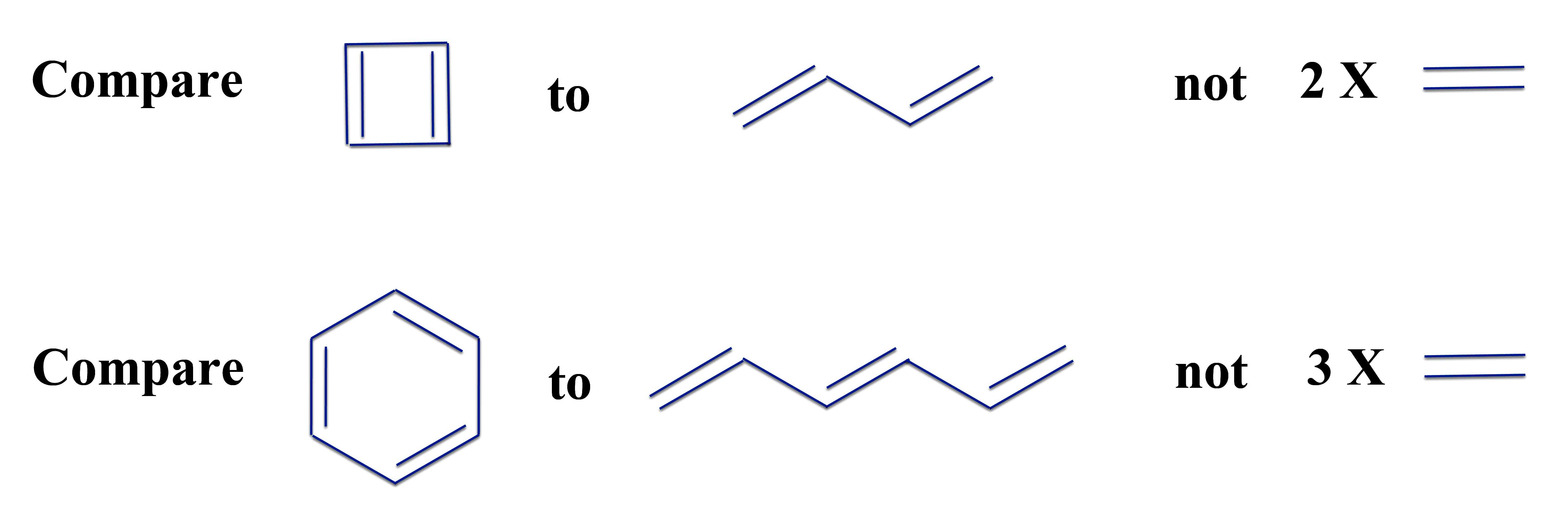
An important point is that the double bonds of a polyene don't have exactly the same energy as that of ethylene. An even more complicating factor is that in the straight chain polyenes, you have some of the double bond electrons spread out into where we draw single bonds. So the single bonds of polyenes don't have the same bond energy of compounds with pure single bonds either. And a final difficulty is that in an annulene you have one extra polyene "single" bond in the classical structure. So what can we do?
We've shown that the PMO method lets us calculate the energy difference when you bring an R-S pair together. But you can bring them together in more than one way. For instance, we've already shown you can bring two allyl radicals together to form benzene by joining both ends of the radicals together.
But what if you just join one end of the radicals? Then you get linear hexatriene - the reference structure for our new definition of benzene's aromaticity!
Allyl to Hexatriene: PMO Energy
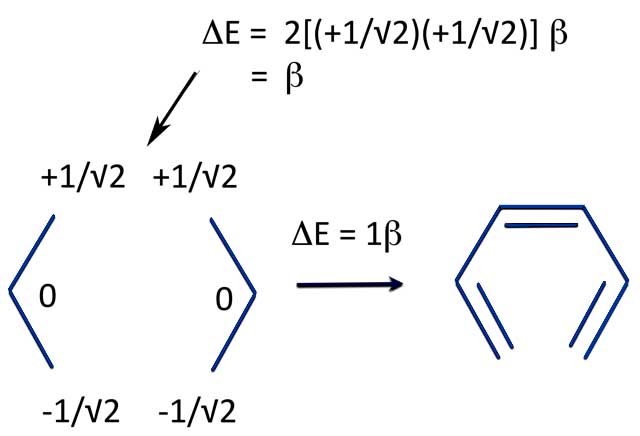
And since we've already calculated the energy of forming benzene from two allyl radicals, we can now calculate the energy of ring closure.
Benzene: Michael's Resonance Energy
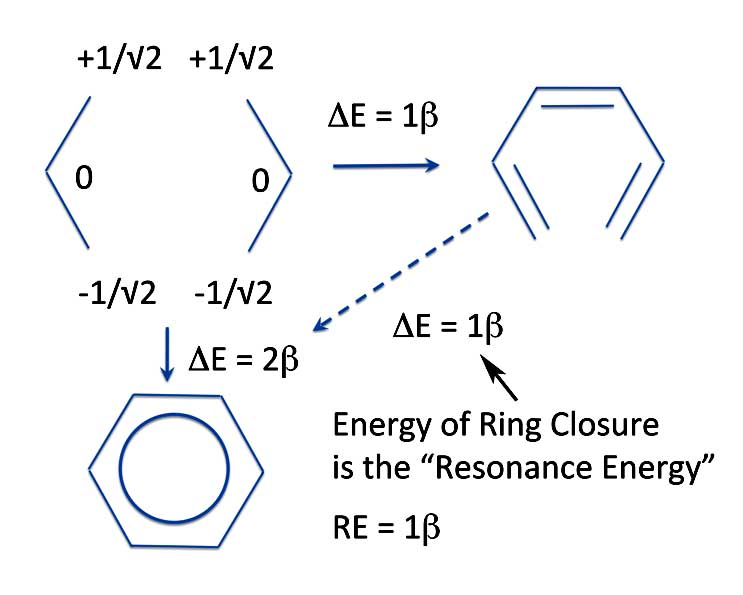
And this energy of ring closure is what Michael said is and should be our definition of resonance energy. So the resonance energy of benzene is not 2β that Erich calculated, but the PMO value of ring closure, 1β.
In calculating the PMO energy of ring closure, we do not need to worry about the extra "single" bond of the annulene reference structure. Michael's PMO method takes care of that automatically. That's because the overlap of the p-orbitals and the subsequent energy change when forming a "single" bond in a conjugated hydrocarbon is what is known as a second-order perturbational effect. The energy calculated when using the R - S pairs of two radicals is a first-order perturbational effect. So resonance energy by Michael's definition is actually the first order energy of ring closure. To explain this in greater detail we would have to delve more deeply into Michael's theory. This is something we said we wouldn't do - so we won't..
You can also calculate the energy of ring closure using the alternative R-S pair of the pentadienyl and methyl radicals. The energy will not be exactly the same as from two allyl radicals, but it's pretty close; 1.15β compared to 1β. But in any case, the resonance energy is positive and benzene is correctly identified as an aromatic compound and more stable than the open chain linear analog.
Pentadienyl + Methyl -> Benzene
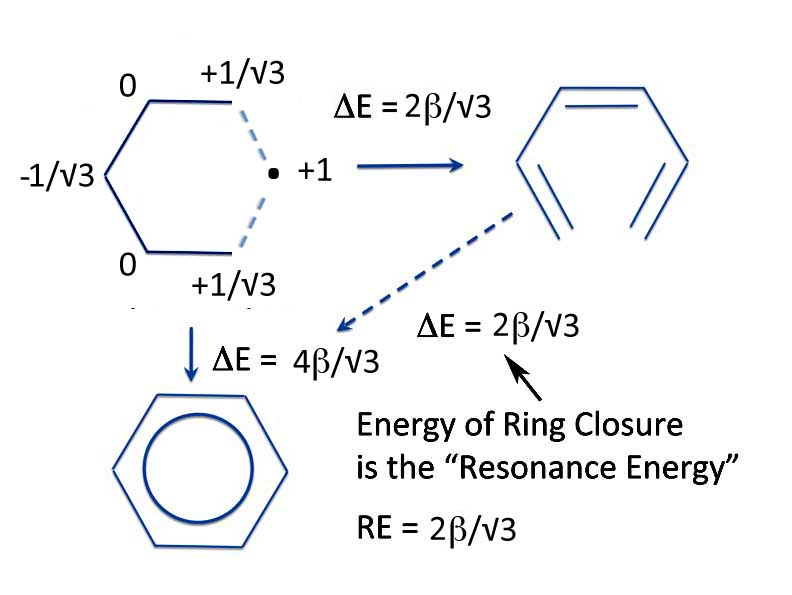
Now we move on to where the PMO method shows some real advantage. If we accept this definition of resonance energy - that resonance energy is energy of ring closure - we can calculate the aromaticity of multicyclic, that is polycyclic, hydrocarbons. Without drawing any resonance structures, we can determine both the overall aromaticity of the molecule as well as the aromaticity of the individual rings.
For instance, let's an R-S pair made from two pentadienyl radicals joined in three different ways:
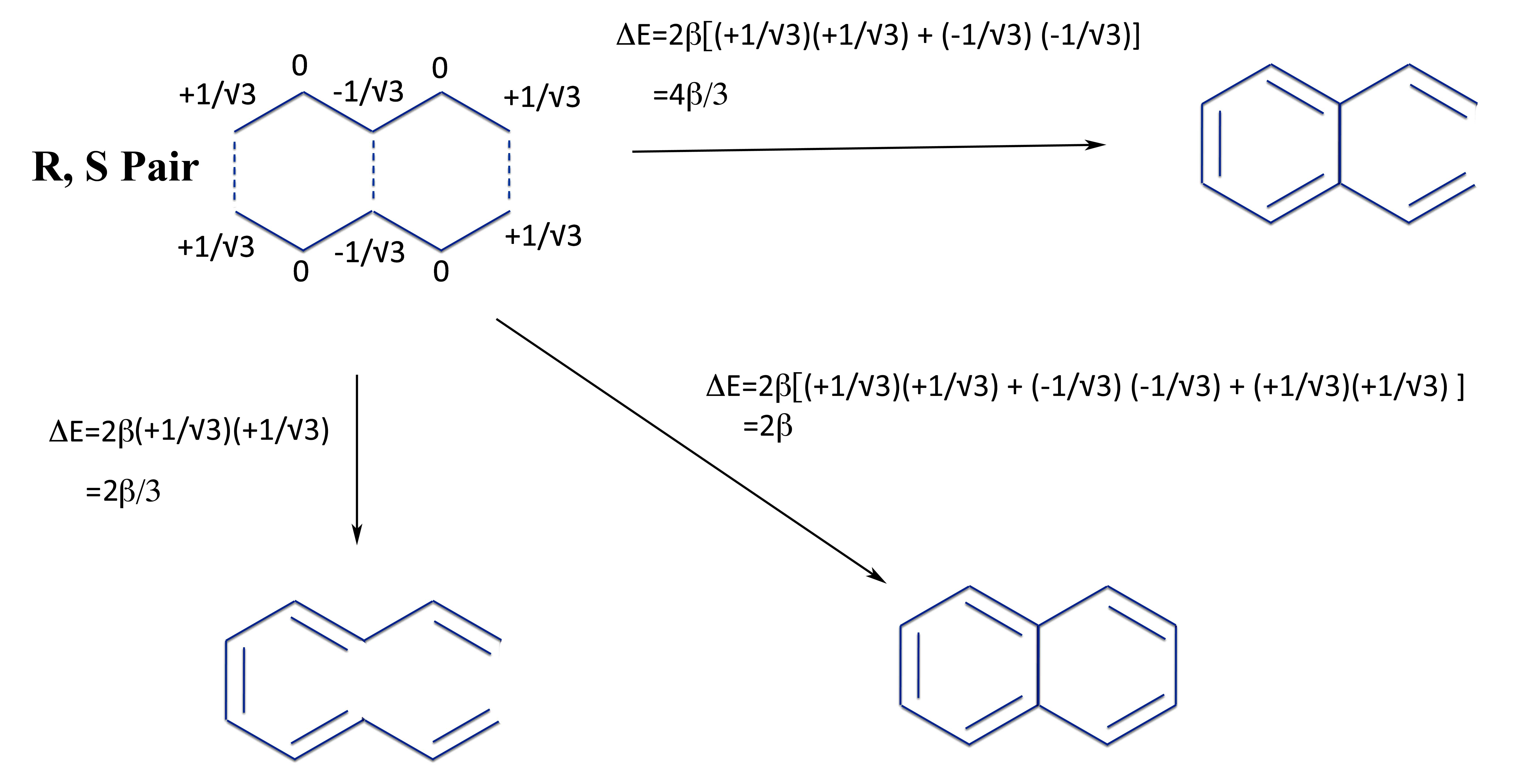
We can calculate the energy change to form the linear polyene (bottom left), a monocyclic di-vinyl benzene (upper right), and the bicyclic aromatic compound naphthalene. This now allows us to calculate the total resonance energy and that of the individual rings of napthalene.
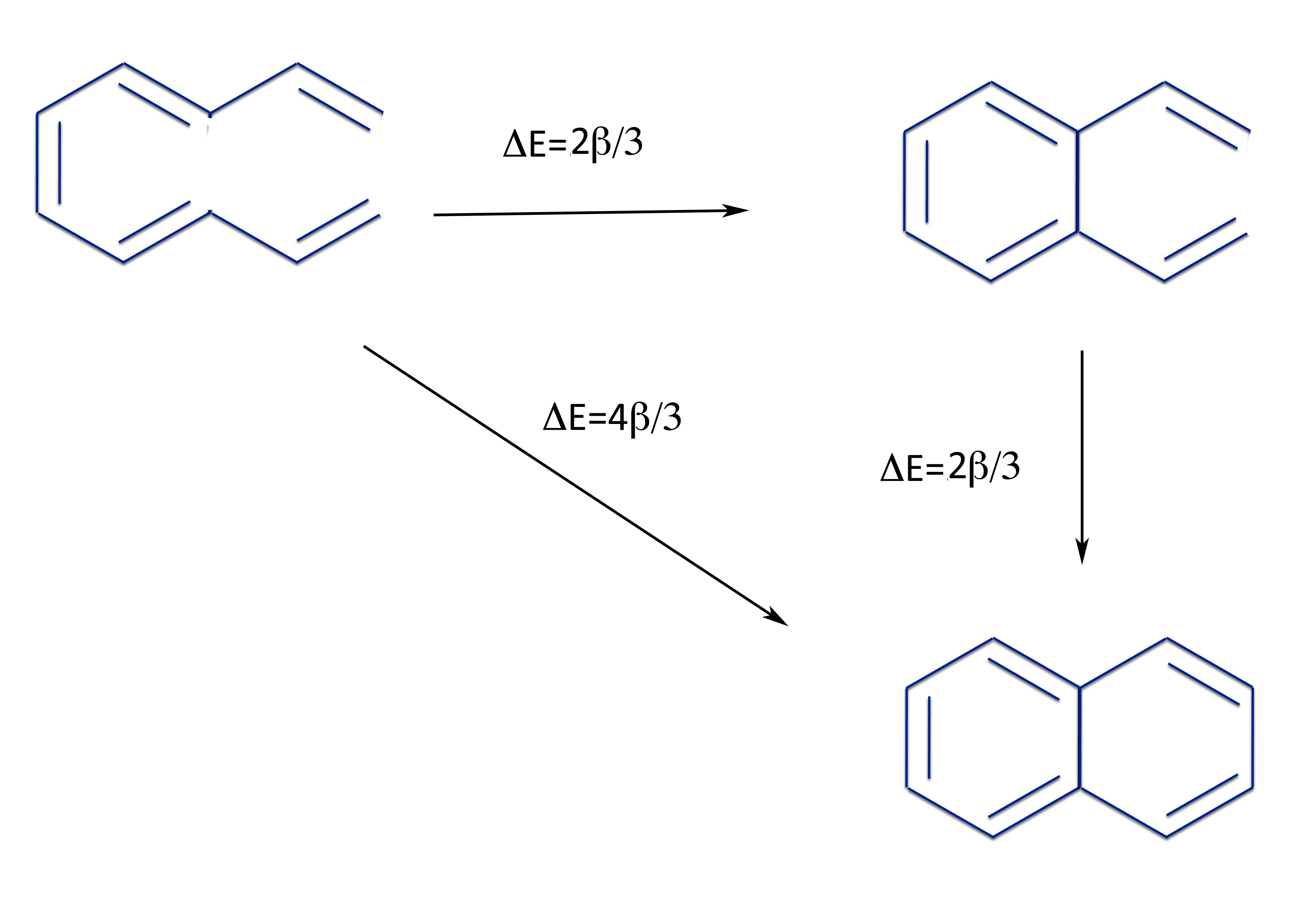
So not only is napthalene aromatic with a total resonance energy of 4β/3, but both rings are equally aromatic (which they must be by the symmetry of the molecule).
Well, that's fine. But what about something like cyclobutadiene, that troublesome molecule we say Huckel theory doesn't really tell us anything about?
Well, you do exactly the same thing. Take an R-S pair - in this case allyl and a methyl - and calculate both the energy of forming linear butadiene and cyclobutadiene. Then we can calculate the energy of ring closure. And look what we get:
Butadiene and Cyclobutadiene: Michael's Resonance Energy
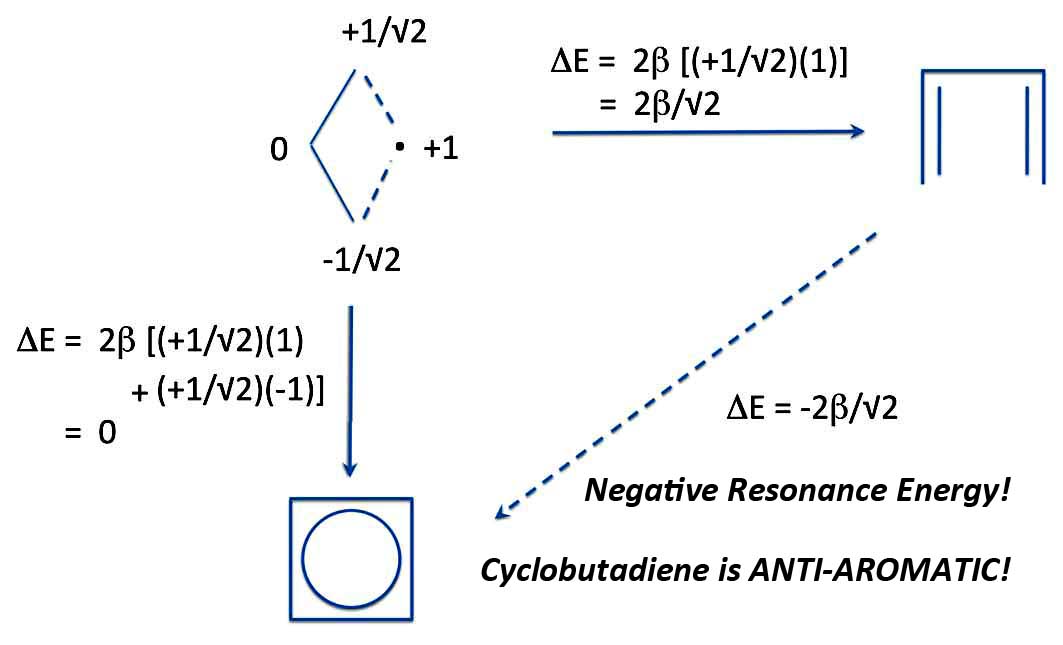
Yes, the energy of ring closure is NEGATIVE! So cyclobutadiene is not just nonaromatic, but ANTI-AROMATIC!. That is less stable than the open chain reference structure.
[Though it is sometimes believed that Michael coined the word "anti-aromatic", that isn't true. That honor goes to Professor Ronald Breslow of Columbia University.]
So we see that the PMO method has the reference structure built in for calculating resonance energies. Now using simple middle school math you can calculate resonance energies of all annulenes as a simple formula. That is for any annulene of ring size n, the energy of forming the straight chain polyene is:
| Energy of Polyene Formation (β) | = | (-1)n/2+12β/√ n/2 |
| = | (-1)n/2+12√ 2 β/√ n |
So it follows that the energy of ring closure, the resonance energy is:
| Resonance Energy (ΔE of Ring Closure, β) | = | (-1)n/2+1√ 2 β/√ n |
Now if you plot these resonance energies you get a much more interesting graph. And one that is much more in keeping with the chemists' notion of what aromaticity should be.
Annulenes: Michael's Resonance Energy
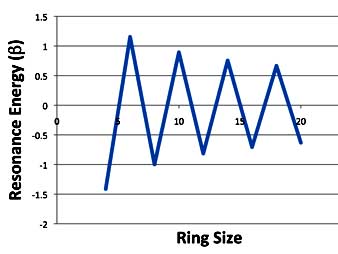
So according to the PMO theory, 4n + 2 annulenes are aromatic, 4n annulenes are anti-aromatic, but as you get to higher ring sizes, the two types of compounds converge toward each other.
It's been noted that a better indication of stability or reactivity is not the total resonance energy, but the resonance energy per pi-electron or REPE. So you divide the total resonance energy by the number of pi-electrons (i. e., the number of carbon atoms in the ring). In that case, plotting the REPE of the annulenes produces the graph:
Annulenes: Michael's Resonance Energy Per Pi-Electron (REPE)
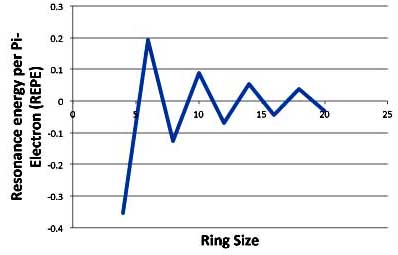
Using REPE shows that the stability of the aromatic and anti-aromatic annulenes fall off fairly rapidly. So there is less stability for larger aromatic rings and less instability for the larger anti-aromatic rings.
Michael's PMO theory also lets us compare the relative degree of aromaticity of two isomeric compounds. For instance, let's find out which compound is more aromatic, anthracene or phenanthrene.
If you want to use resonance theory you have to draw all the possible resonance structures. The compound with the most resonance structures is the most aromatic. However, as you get to larger molecules, you have to draw more and more resonance structures. So it soon becomes hard to keep track of whether you're accidentally leaving some out. And besides, we saw that just because you can draw resonance structures, it doesn't even mean the compound is aromatic.
But with the PMO method, it's a snap to compare the two molecules. Just take two benzyl radicals as your R-S pair and make both molecules. The answer is immediately and easily obtained.
Phenanthrene and Anthracene
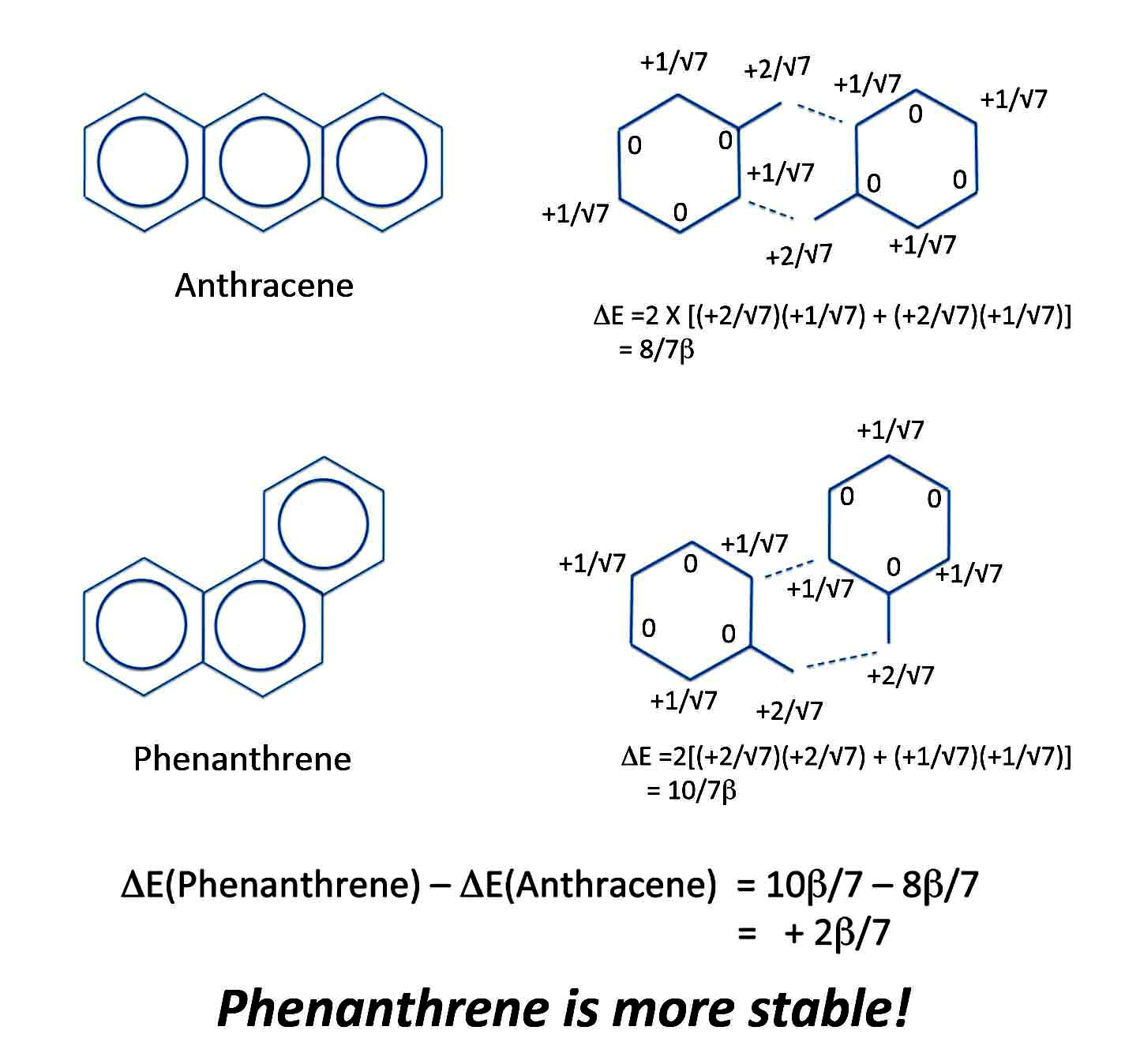
Of course, there are other ways to construct anthracene and phenanthrene from the same radicals. But whichever way you try, you'll get the same - and correct - answer.
Return to Pyrene
OK. Now armed with the PMO Method we can now attack the Problem with Pyrene. We do it exactly as the annulenes
First, we draw the structure.

But for the PMO method we leave out the double bonds.
Now what we do is decide on how to break the molecule up into two odd-number radicals that you can draw 1) as a linear non-cyclic polyene and then 2) close it to form our polycyclic compound, pyrene.
Again there are many ways to do this. But we'll keep it simple and make our R-S pair from a one carbon radical and with a 15 carbon radical as below.
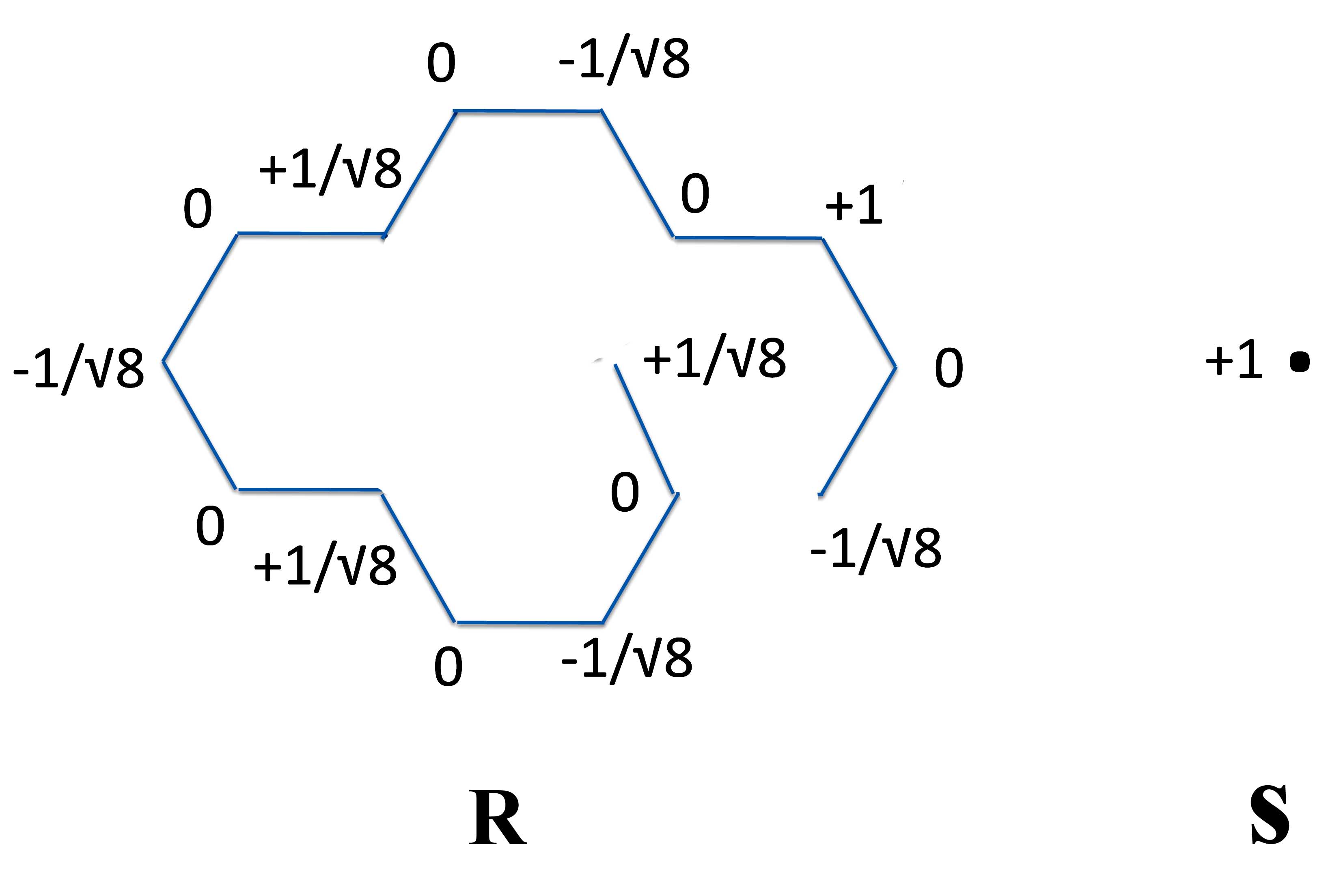
At this point we put them together to form the basic pyrene shape.
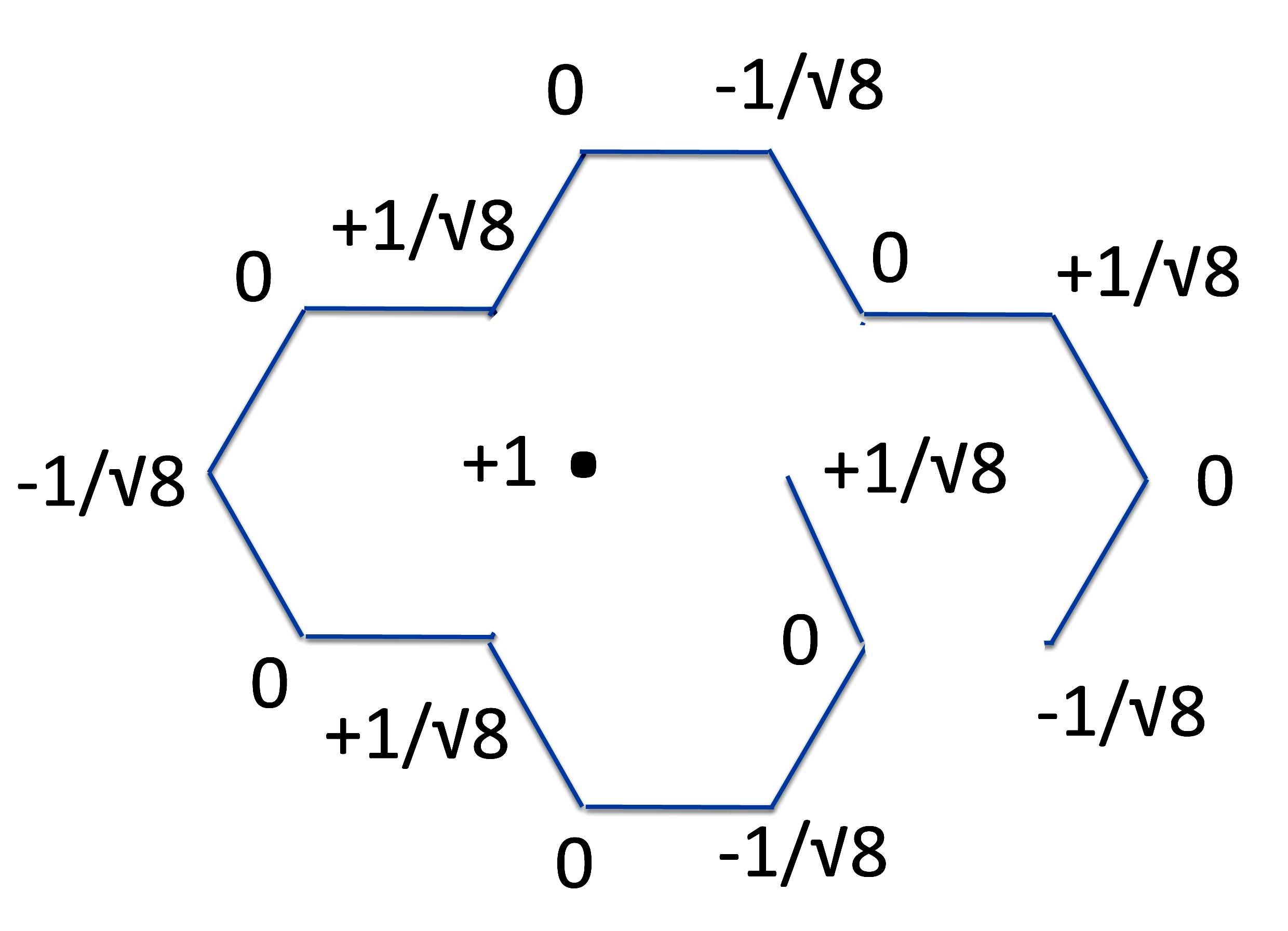
And form the linear polyene.
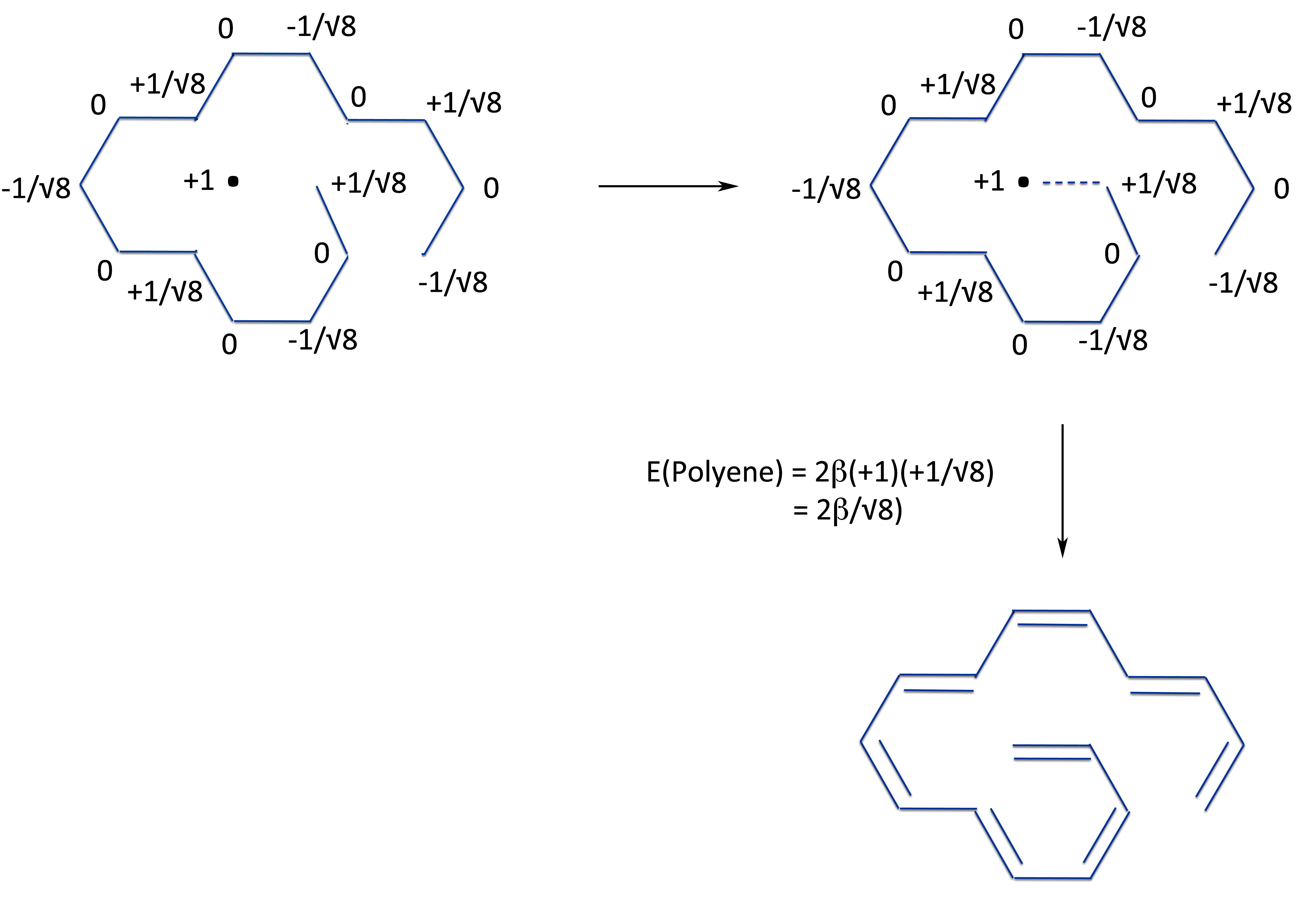
And from the same two radicals, we now form pyrene.
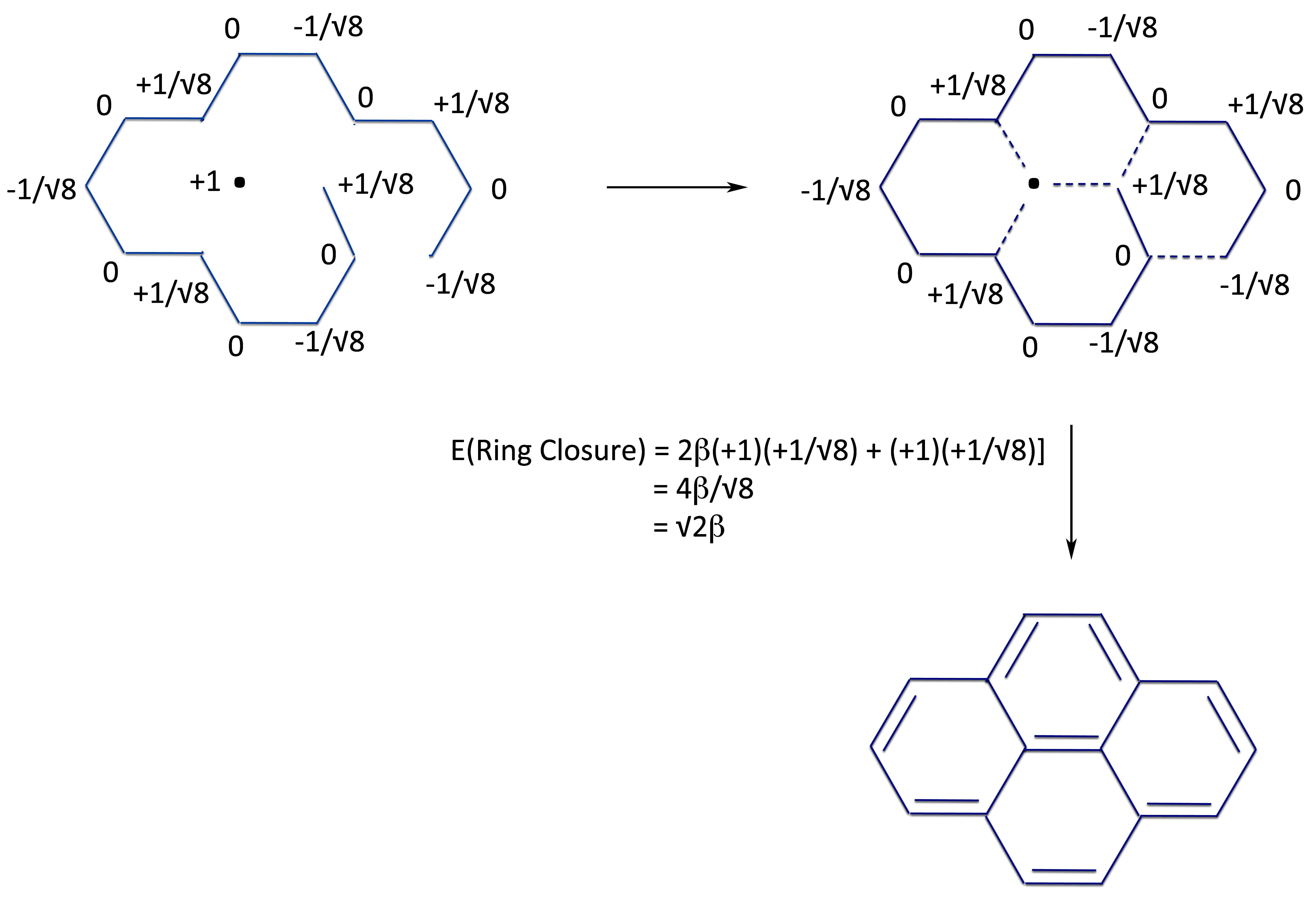
Which by simple grade school mathematics lets us see that the energy of ring closure, ergo, the resonance energy of pyrene is:
So pyrene has overall a positive resonance energy and hence is an aromatic compound!
And the individual rings?
What we have to do is create a structure where we can close each ring to see if the ring closure is positive or negative. Although there are four rings, the symmetry of the molecule means we only have to examine two rings.
So to proceed.
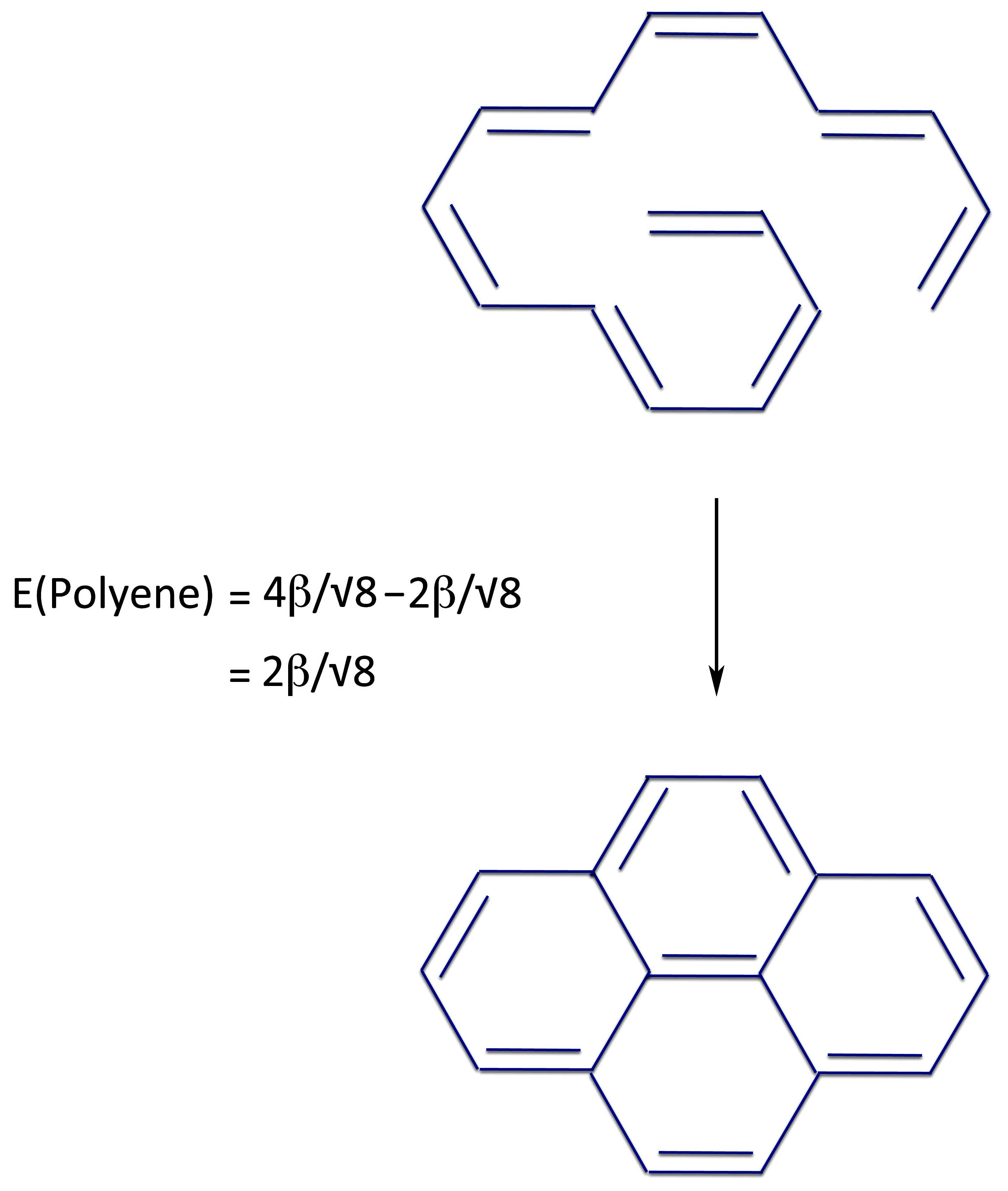
We saw that with naphthalene both rings were aromatic. So we can add a butadiene chain at one point and an ethyene group (i.e., vinyl) at another. Since we've formed no new rings, both rings on the naphthalene part are still aromatic. You can prove this easily with the PMO method, a proof that will be left for the reader.
Next we have to make our two PMO radicals that can create this structure. One way to do that is:
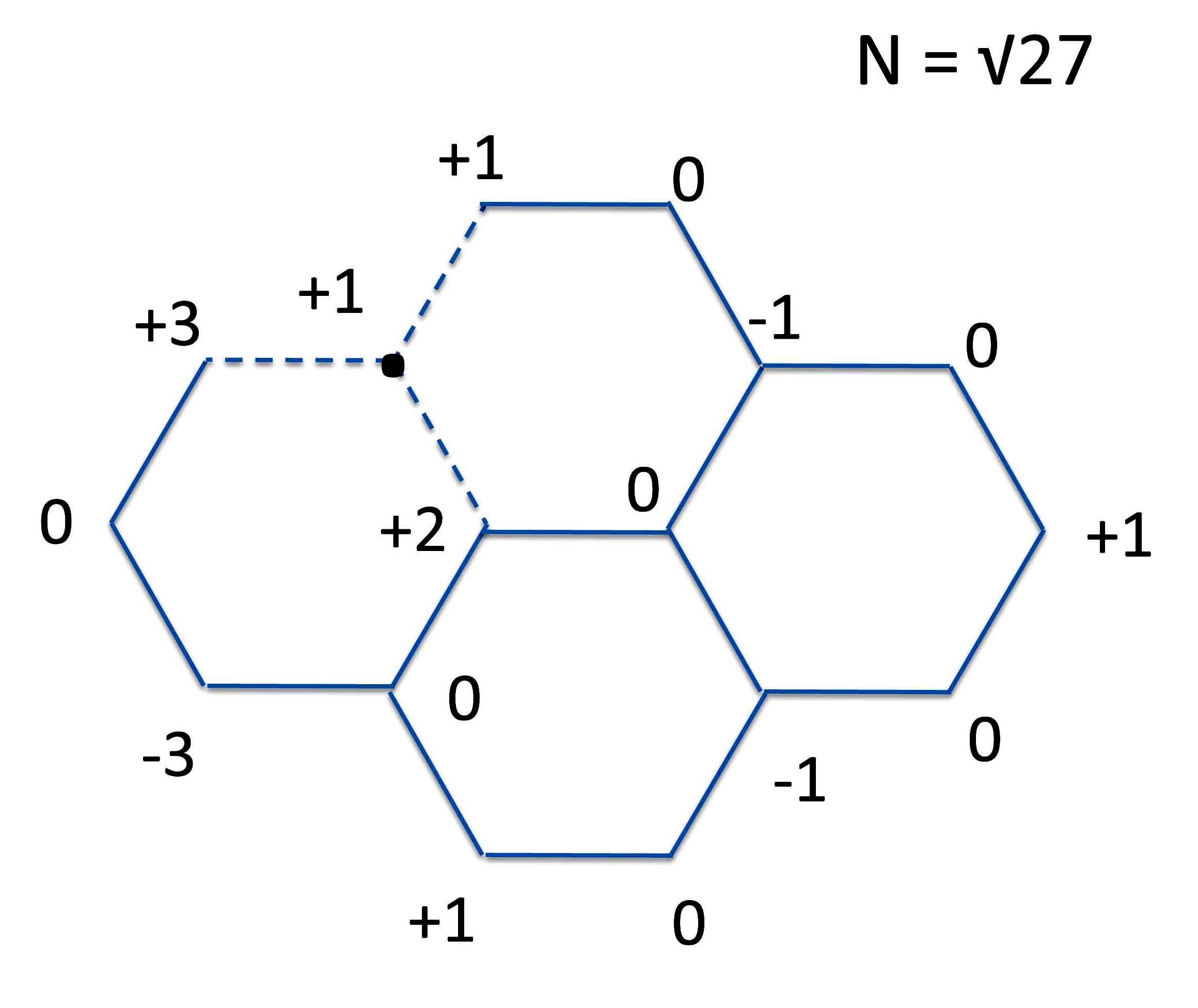
This allows us to set up the scheme:
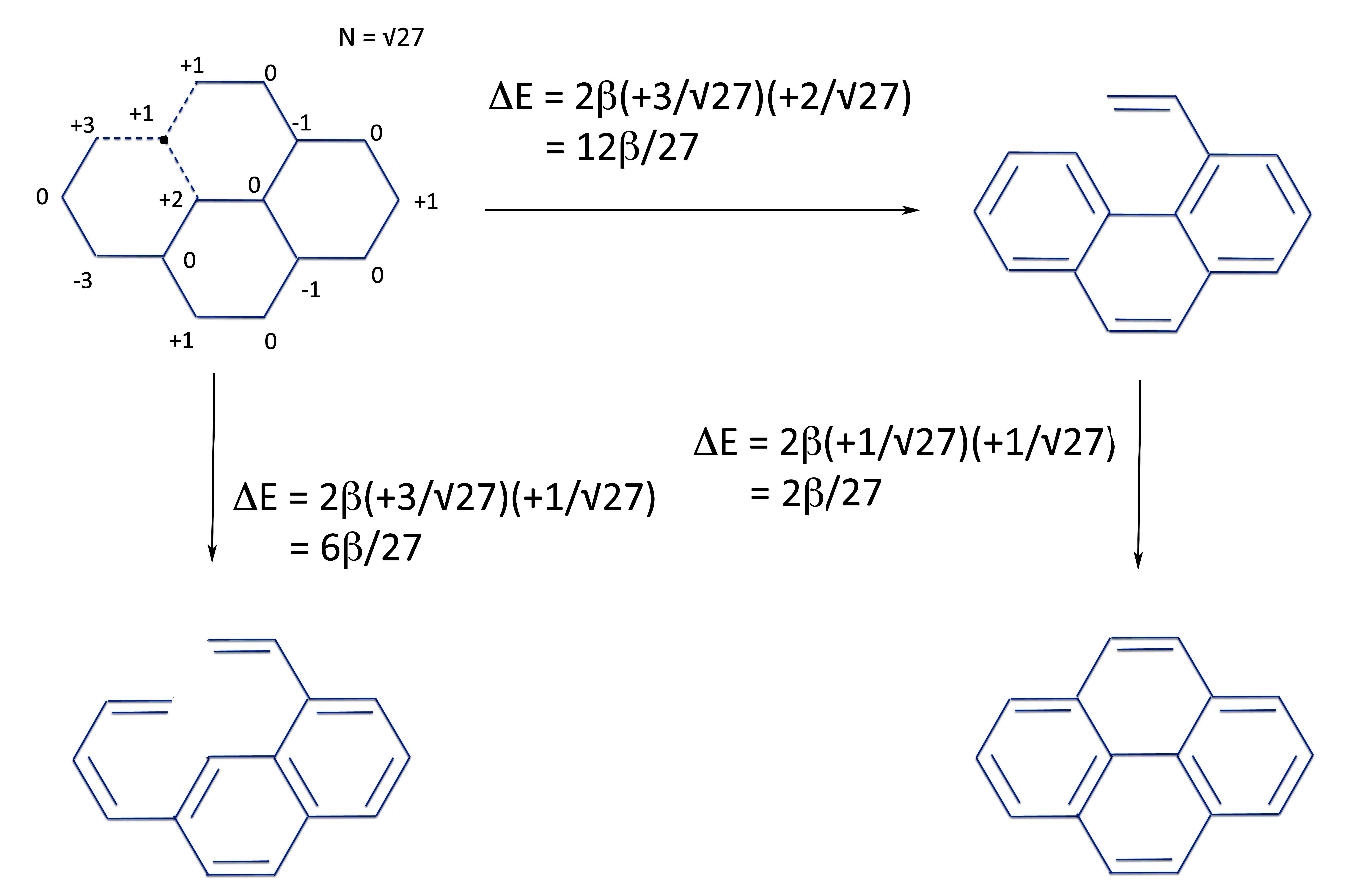
Which in turns gives us the energies of the ring closures:
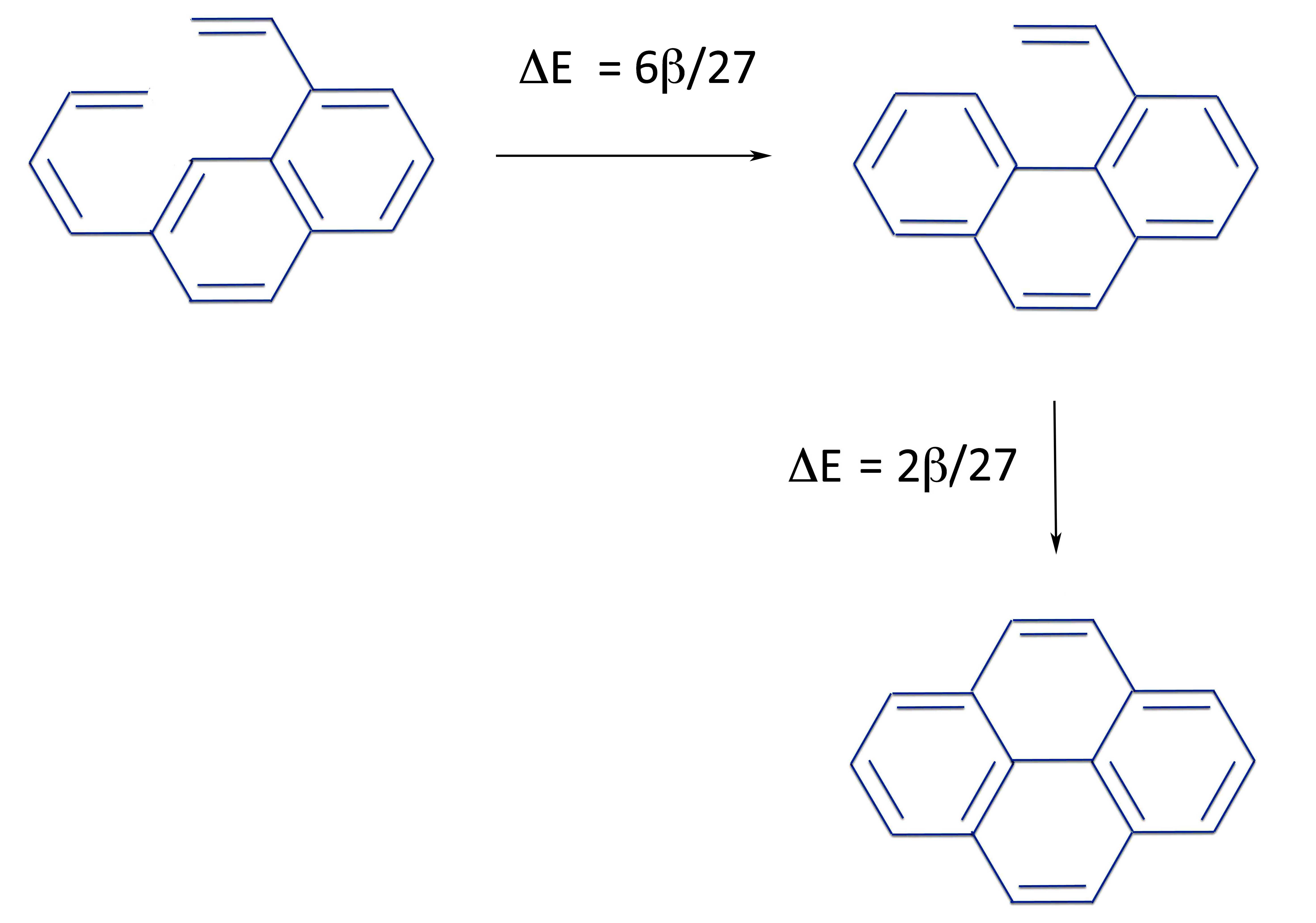
So there's no way out of it. Pyrene - with 4n electrons - is completely aromatic.
A Final Example
Another case showing how the PMO method has advantages over resonance theory is the way it handles the odd-ball compound, benzycyclobutadiene.
Benzocyclobutadiene
Is it aromatic or anti-aromatic?
Well, let's take a look. First we create an R-S pair that can 1) produce a straight chain polyene and then 2) close up the rings to get our compound of interest. By now that should be easy and we find we get:
Benzocyclobutadiene
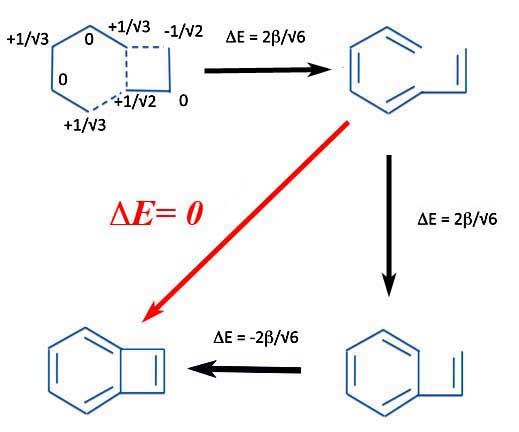
That is the energy of ring closure - the resonance energy - zero.
The conclusion is, as they say, very interesting. If you get no change in energy from the open chain polyene to benzocyclobutadiene we can conclude only one thing. The compound is neither aromatic nor is it anti-aromatic. It is a non-aromatic polycyclic conjugated hydrocarbon.
The conclusions, interestingly enough, were exactly the conclusions of some theoretical chemists using much more advanced ab-initio calculations, that is, complicated computer calculations from "first-principles" quantum theory. Based on various electronic characteristics, they said the molecule was neither globally aromatic nor globally anti-aromatic. Exactly what is predicted by the PMO method - a technique developed half a century earlier!
The Real Hückel's Rule
The problem is the original 4n + 2 rule was derived specifically for the monocyclic molecules - that is, the annulenes. So to say all molecules with 4n + 2 electrons are aromatic and those with 4n electrons are not, is simply incorrect reasoning.
Instead aromaticity is determined by the way the atoms are arranged, and not necessarily by the total number of electrons in the molecule. From the way you construct the R-S pairs we can see that a neutral ring with 4n + 2 carbon atoms will have extra stabilization compared to the linear structure and a ring with 4n carbon atoms less stability. Aromaticity, then, is most meaningful when referring to the individual rings. And Michael's PMO method - with its own built-in definition of resonance - is really the best way to do determine if a ring - or the molecule as a whole - is aromatic.
So yes, Virginia, there are aromatic compounds with 4n π electrons. And pyrene is one of them.
PMO Theory: Where is it?
Surprisingly, even after more than sixty years, and despite the advantages and surprisingly little ambiguity in its implementation, Michael's PMO method has yet to attract a wide group of followers. Crack open any recent organic textbook - even advanced ones - and you'll see resonance structures are still bandied about with much élan; but only a few mention Michael's PMO alternative.
So what happened?
The reasons for the neglect are legion. Part of the problem is simply that Michael - as he himself mentioned - did not widely publicize his ideas. Although he was a teacher (most professors are), he was primarily a researcher who preferred to publish new findings rather than dwell on what he had already done. After all, people could read the PMO papers since they had been published in one of the most widely circulated chemical journals.
The trouble is those papers can still be a bit tough going and even Michael later called them "rather indigestible". The papers are quite mathematical and the information is put in terms of theorems - something sure to scare off a lot of organic chemists. Before they could reach the easy parts, most of the readers had long given up.
It wasn't until 1969 that Michael provided the first really accessible account of the PMO method and then only in a chapter of a book whose title would again scare off many chemists. Then finally in 1975 Michael and a colleague (and former student) issued a complete book on the PMO method alone and which although there was plenty of theory, there were also maximum of examples. By then though, it was - again as Michael himself admitted - too late.
Probably the biggest hindrance for the PMO method displacing resonance theory was, alas, resonance theory itself. For one thing resonance theory required no math while the PMO method required at least some. Resonance theory was also put in terms of that fundamental concept, the chemical bond, and so was easily grasped by struggling undergraduates.
But above all else, resonance theory - as Michael and Charles pointed out - does indeed work, even if they felt it worked for the wrong reasons. And today many advocates of MO theory - at least when teaching organic chemistry - find themselves resorting to resonance structures when explaining or rationalizing some chemical phenomenon. One of the leading chemists of the 20th and 21st century - who as of this writing is still going strong - wrote that as much as he advocated MO calculations, he still found himself going back to resonance structures.
There are other reasons, too, or the neglect of the PMO method. After all, there was the time that Michael was giving a lecture and ...
Well, we'll skip that for now.
But then he once wrote an article that stated the theory that won a famous chemist a Noble Prize was ...
Oh, we'll let that pass, too.
But then once Michael ...
Well, let's just say that Michael was one of the more colorful chemists of the twentieth century. Perhaps we will save the "other reasons" for a later day.
References
With the qualification that Captain Cochoran made on board the HMS Pinafore, CooperToons website never endorses political positions or advocates particular ideologies. Instead it is sufficient to spread accurate and honest information in this day and age of increasing ignorance and superstition.
However there is an official CooperToons opinion that the costs of many scientific books, particularly in the physical and mathematical sciences (and not just textbooks) has climbed to astronomically absurd levels. After all it's kind of ridiculous for scientists, mathematicians and engineers to [gripe] and moan about the dwindling scientific literacy of the American citizen while they're trying to sell their books about science, engineering, for $300. Alas, some of the books used for this essay fell into those nice-to-read-but-just-too-damn-expensive genre.
Fortunately, believe it or not, you can actually go to what are most unusual buildings. Most towns have at least one. They are called public libraries - and may the author die the death of a dog if he lies - there you can actually borrow books for free. And if the book you want is not in that particular library then there are people there (usually very nice and pleasant ladies) who can get you an interlibrary loan which again costs nothing. There is also another official CooperToons position that public libraries should always be with us and not succumb to the if-I-don't-use-it-then-my-taxes-shouldn't-pay-for-it philosophy so common to those who spend their time swilling cheap beer and punching in 24/7 sports channels on their remote.
For those, however, who want personal copies, make sure you shop around. One online vendor of a reference book for this article was hawking the volume for nearly $200. But another bookseller was selling it for a dollar.
Michael J. S. Dewar: A Semiempirical Life, Michael J. S. Dewar, American Chemical Society, 1992. A very well written and entertaining autobiography. Michael mixes stories of his childhood, student days, and professional life with quite a bit about his chemistry. Used copies are available at moderate prices.
"Michael J. S. Dewar: A Model Iconoclast", Eamonn F. Healy, Pioneers of Quantum Chemistry, E. Thomas Strom, Angela K. Wilson (Editors), American Chemical Society, 2013. This book has some interesting stories about the way Michael interacted with his fellow chemists - sometimes not always smoothly. There are also good chapters about Charles Coulson and Christopher Longuett-Higgins who were colleagues and friends of Michael.
The PMO Theory of Organic Chemistry, Michael J. S. Dewar and Ralph C. Dougherty, Plenum. 1975. A highly detailed book of the PMO method which focuses on applications.
The Norton History of Chemistry, William H. Brock, W. W. Norton, 1993. A lot about the development of organic chemistry theory.
"Robert Robinson: 13 September 1886 - 8 February 1975", Biographical Memoirs of the Royal Society, Lord Alexander Todd and Sir John Cornforth, Vol. 22, pp. 414-527, (1976). The section of theoretical chemistry was actually the work of Michael and as Sir John and Lord Alexander said they largely kept to his original wording. It is most interesting that the reasons Michael gives that Sir Robert's contributions to the theory of organic chemistry are not recognized are almost verbatim the reasons Michael gave that his own PMO theory has never been widely accepted and used.
"In Memoriam: Michael J. S. Dewar," http://www.utexas.edu/faculty/council/1998-1999/memorials/Dewar/dewar.html.
The Molecular Orbital Theory of Organic Chemistry, Michael J. S. Dewar, McGraw-Hill, 1969. It would have been nice if this had gone through later editions and much of the information is quite dated. Also the book was published before Michael's most important and influential high level theoretical research was undertaken.
The book still has real value, though, particularly its rigorous derivation of quantum mechanics (using Heisenberg's method and Dirac's notation) and the Roothaan self-consistent field equations. Michael also discusses in some detail how he set up the equations for his own calculations and so the reader can get a good idea of how to do the nuts-and-bolts of semi-empirical quantum calculations. Used copies are available. The author's personal copy - in good condition - was purchased for $1 from a bookstore in London. The trans-Atlantic shipping fee was $7.
Two Lectures on an Outline of an Electrochemical (Electronic) Theory of the Course of Organic Reactions, Robert Robinson, Institute of Chemistry, 1932. Sir Robert's classical theory.
"Benzocyclobutadiene: The Question of Structures, Magnetic Shieldings, and Aromatic Character", International Journal of Quantum Chemistry, Vol. 90(2), pp 616-628, 2002. The PMO calculation reported above was completed before this reference was located. Hence, the PMO prediction we gave above is indeed a true prediction - not post-hoc.