Linus Pauling
and the
Battle of the Quantum Calculators

Linus Pauling? Oh, yeah. The Vitamin C guy. According to Linus, just take megadoses of Vitamin C, and you'll live much longer and healthier. You'll have fewer colds and be less likely to die of cancer. Not only that, Linus said, but for patients already afflicted with cancer, gram quantitites of Vitamin C will cure the disease 75 % of the time.

Now we have to be honest and say that Linus's claims about Vitamin C are not swallowed (no joke intended) by virtually all modern medical practitioners. Instead, many feel his advocacy of the "orthomolecular" theory of health has made Linus one of the more regrettable figures of twentieth century medicine. They point out the orthomolecular approach is just another of the simplistic theory-driven health-nut fads with lots of feel-good buzzwords, but which ignores massive experimental evidence to the contrary. Worse, it actually discourages patients from seeking proper therapies.

Linus's politics, too, were enough to send your average American Joe and Josephine Blow into spittle flinging diatribes. Why should we honor a man so obviously opposed to American ideas who reveled in rubbing elbows with the Commies?

Well, for one thing, Linus was not opposed to American ideas and was far more a believer in the principles of the American constitution than a lot of our more fervent patriotic chest-thumpers. In fact, Linus even volunteeringly signed a loyalty oath to the United States, and we must wonder how many HUAC members ever did that. Instead, if you actually listen to what he said - and not what some people said he said - you'll find he did not disagree in basic principles from those who are sometimes looked on as his political opposites.

For one thing, Linus did believe - and he said so - that we needed nuclear weapons capability as a deterrent, not only to prevent nuclear war but also to discourage conventional war. As far as accepting the Lenin Peace Prize from the Soviet Union and attending various political congresses where the Russian spouted their own world view and trashed the Americans, this did not mean that Linus believed the Soviet system was better than ours. Au contraire, he stated flat out that his problems with the government - being followed, wire tapped, and denied permission to travel abroad - were nowhere near as bad as what the dissident Soviet scientists were subjected to. Also Linus was awarded the Nobel Peace Prize in 1962 for the essentially the same thing as the Lenin Prize. Ironically, in an action coming close to that of the Soviets when they prevented Boris Pasternak from accepting the Nobel Prize in Literature ("officially" Boris - quote - "declined" - unquote - the Prize), the US State Department seriously considered denying Linus the permission to travel to Stockholm. And we should remember that virtually all of what Linus had advocated - banning above ground nuclear weapons and reducing the number of nuclear weapons in the Soviet and US arsenal - were eventually adopted.

But even not counting the Vitamin C controversy, Linus was clearly wrong on some things. Certainly massive nuclear stockpiles haven't really dented casualties from conventional warfare. And then there was the time ...

Well, we'll get to that later.

But it's natural to ask. Out of all his awards and honors and accomplishments, what was it that Linus was most proud of? Was it his advocacy of the orthomolecular approach to health? That he first deduced the three dimensional structure of proteins? Could it be his winning of two unshared Nobel prizes (he also got one in chemistry in 1954)?

Nope, none of these. And his response may surprise you.

Linus was most proud of a series of papers he wrote titled "The Nature of the Chemical Bond." The first paper was published in the Journal of the American Chemical Society in 1931 when Linus was only 30, and it was indeed these papers that pushed him into the international scientific spotlight.

All right. So what did Linus actually do?

Despite the tongue twisting titles - the first paper was subtitled "Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules" - Linus's paper first took some - quote - "simple" - unquote - solutions to the famous Schrödinger Equation. Then he found that by simple algebra you could combine them in entirely new ways that would explain the structures of complex organic molecules. What Linus wrought became (and still is) fundamental to understanding molecular structure and is universally taught even in introductory chemistry courses. These papers did, ironically, get him involved in even more controversy. But as we all know, controversy never bothered Linus.

Erwin Schrödinger: Not a Cat Lover

Today a lot of people know about Erwin Schrödinger. Just as Linus is the guy with the Vitamin C, Erwin was the guy with the cat. That is, the cat that we can't tell whether it's alive or dead unless you either killed it or didn't.

Actually Schrödinger's cat is an amusing paradox of the type that keep cropping up in quantum mechanics. But that's not the most important thing about Erwin. He was in fact one of the originators of quantum mechanics, a branch of science which has the distinction of being, despite what some of the more oddball websites claim, one of those theories that we can accept as completely, entirely, and absolutely true.

Erwin's equation is surprisingly easy to derive. But to spare those who object to having nerdiness forced on unsuspecting readers, we will relegate the derivation to the Appendix at the end of this essay (to jump to the Appendix just click here). But briefly what Erwin did was to take the classical equation for waves (which govern how strings on musical instruments behave) and then substitute for the wavelength of the string, λ, the equivalent expression for mass and velocity of a particle that was in turn derived by the French physicist, Count Louis de Broglie.

λ = h/mv

Here h is the famous Planck's constant which is equal to
0.000000000000000000000000000000000662606957 meters-squared-kilograms per second. And m is the mass in kilograms of whatever object your interested in, and v is it's velocity in meters per second.

Then with some surprisingly simple math you get the equation:

(-h²/2m)(∂²ψ(x,y,z)/∂x² + ∂²ψ(x,y,z)/∂y² + ∂²ψ(x,y,z)/∂z²) + V(x,y,z)∂ψ(x,y,z) = Eψ(x,y,z)

which even a child of four can recognize as a second order differential equation in three dimensions. This equation, we should point out, applies to everything from subatomic particles to ocean going ships and on up to the largest objects in the universe.

The goal in quantum mechanics is to find equations that fit in place of ψ. Here E stands for the total energy of the system. V(x, y, z) is itself an equation that represents the potential energy. Of course, the actual equation ψ depends on what system you are working with.

For instance, if you have a car that weighs 1000 kg and it's on a mountain that rises 3380 feet above the valley floor, your potential energy function is:

V(x,y,z) = 9806.65 X (z - 1000)

where z is how high you are (in meters). So the Schrödinger equation for your car is simply:

(-h²/2m)(∂²ψ(x,y,z)/∂x² + ∂²ψ(x,y,z)/∂y² + ∂²ψ(x,y,z)/∂z²) + (9806.65 X [z - 1000])ψ(x,y,z) = Eψ(x,y,z)

Of course, the monkey wrench is that with very few exceptions you can't solve the equation. So what, we ask, is the point?

Well, even when you can't solve the equation exactly you can often determine some general characteristics of the system you're interested in. As far as atoms go, the Schrödinger equation does tell us that the electrons are found only in discrete energy levels. When all the electrons are packed in the lowest possible levels you have the ground state of the atom. Bump the electrons up, and you get excited states which among other things, gives us neon lights, bug zappers, and ghost lights along dark country roads.

Now there is one system that does have an exact solution. That's the hydrogen atom. This is simply an electron moving around a proton and is the simplest atom possible. We can, in fact, get the expressions for ψ that tells us all about the atom.

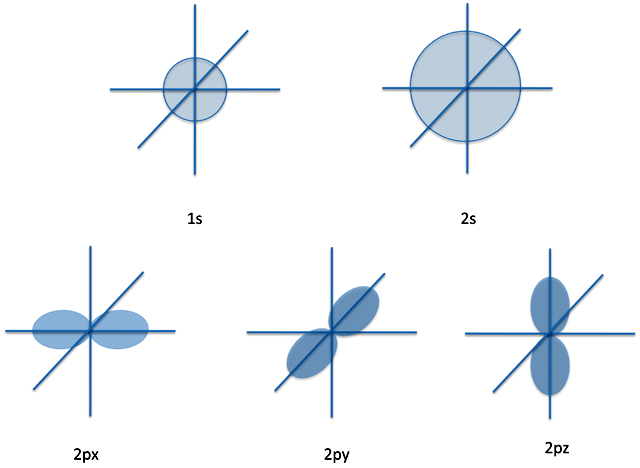
For instance, ψ - the wave function - for the lowest energy level of hydrogen atom is a simple exponential function. This function is labeled 1s and is written (briefly) as:

1s(x, y, z) = A × e^{-b × (x2 + y2 + z2)1/2}

where again A and b are constants (which we won't specify) and x, y, and z are the coordinates of the electron. This wave function defines an orbital for the electron to move around in, an orbital which is - with some conceptual simplification - a sphere.

Now at the next energy level, the electron has four orbitals to choose from. One is, like the 1s orbital, spherical and is called the 2s orbital. But the others are dumbbell shaped and lie along the x, y, and z axes. These are called the 2p_x, 2p_y, and 2p_z orbitals.

So to summarize, for the ground state and first excited state of hydrogen the Schrödinger equation gives us pictures like:

Although you can't solve the Schrödinger equation exactly for more complex systems - that is, for atoms with more than one electron - you can construct approximate solutions based on our equations of the hydrogen orbitals. The approximate solutions are constructed by twiddling with the hydrogen orbitals (such as changing the values for the constants A and b) and can be used as a starting point to construct not too bad guesses for the wave functions of other atoms.

As a chemist though Linus was more interested in combinations of atoms - that is, molecules - than single atoms. Of course, Linus was interested in atoms and molecules both, but mostly molecules.

So let's make a molecule - methane (CH₄) - out of the orbitals of carbon and hydrogen. One way to do this is to start off with one carbon atom. In a simple picture of the ground state of an isolated carbon atom, we have two electrons in the 1s orbital, two electrons in the 2s orbital and you divide the remaining two electron between any two of the three available p orbitals. If you dredge up the memories of your chemistry classes, this is the 1s²2s²2p² electronic configuration.

For reasons that may be clearer later it is best to use another configuration to make methane. So we'll still leave the two 1s electrons where the are but bump one of the 2s electrons into the empty p orbital. So we have the 1s²2s¹2p³ (or more exactly, 1s²2s¹2p_x¹2p_y¹2p_z¹) configuration with four outer shell electrons each with its own orbital. It is these outer shell electrons - the valence electrons - that form the chemical bonds.

Now to make a molecule from one carbon atom and four hydrogen atoms you can stick a hydrogen on each orbital that will "maximize" the overlap of the orbitals. Do that and you get something like:

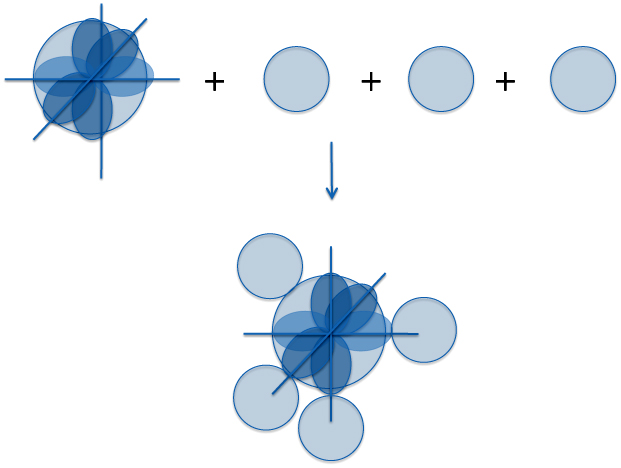
There's just a wee bit of a problem. If you keep with the idea of letting the hydrogen atoms overlap with the individual carbon orbitals most effectively, then the three hydrogen atoms on the p orbitals are separated by angles of 90^o. This means that three of the four carbon-hydrogen bonds are at 90 degree angles to each other. But unfortunately, that's not the case. Methane has four equal bonds all separated by 108.48 degrees. In other words, methane is a tetrahedral molecule. So at first glance the Schrödinger equation doesn't even work for one of the simplest of molecules. But this is where Linus stepped in.

The Hybridization of Erwin

So if the atomic orbitals on carbon don't (at least at first glance) give us the right geometry for methane and other organic molecules what can we do? Well, this was the whole point of Linus's papers.

After Linus got his Ph. D. he was awarded a Guggenheim Fellowship to study quantum mechanics in Europe. His main teacher was Arnold Sommerfeld but he also met the originators of quantum mechanics, Werner Heisenberg and even Erwin Schrödinger himself. At that time, chemists tended not to go in for - quote - "advanced mathematics" - unquote. But since Linus had gotten his undergraduate degree in chemical engineering, he had the wherewithal to understand the actual intricacies of quantum calculations. When he got back to CalTech - now as a professor - he was able to put his knowledge to good use.

Linus understood that if you have a series of solutions to the Schrödinger equation then linear combinations of the solutions are themselves solutions. So he realized that if the orignal hydrogen orbitals couldn't explain the structure of molecules, perhaps he could take the s and p orbitals and combine them to form new hybrid orbitals that would do the job.

There are many ways to combine the orbitals, but there are four combinations that do what Linus needed. They are:

φ₁ = s + p_x + p_y + p_z

φ₂ = s + p_x - p_y - p_z

φ₃ = s - p_x - p_y + p_z

φ₄ = s - p_x + p_y - p_z

All of the various φ_i are called sp³ orbitals since each is made from one s and three p orbitals.

All though the s and p orbitals have different shapes, the new sp³ orbitals look alike. They just point in different directions.

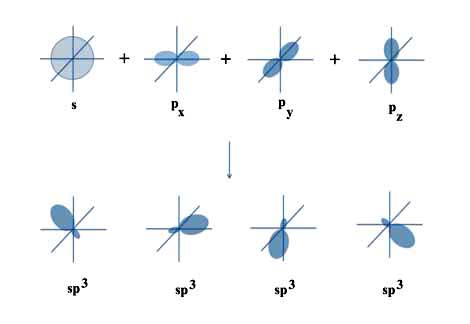
But what is important is that Linus's sp³ orbitals are all separated by the required 108.48^o and are all centered on the same carbon atom.

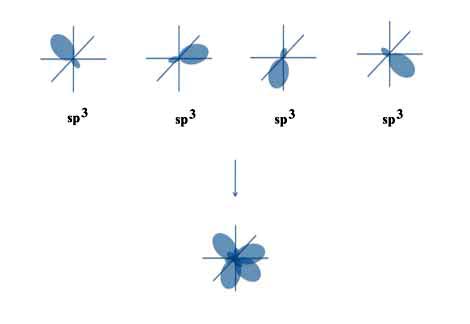
And if you add the hydrogen atoms at the end of each sp3 orbital, everything fits perfectly.

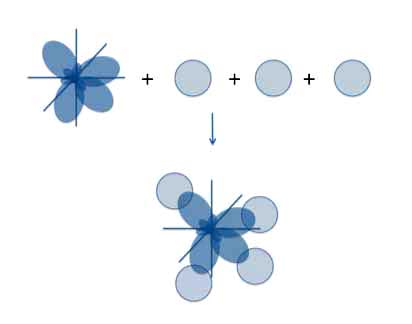
which gives us the correct structure of methane.

How about that?

So Linus's articles - what he was most proud of - showed us how a simple combinations of the orbitals from the Schrödinger equation accounts for the mystery of the famous "tetrahedral" carbon atom, the atom which itself explains so much chemistry.

Linus also developed other types of hybridizations to explain other molecular structures. You can, for instance, take one s orbital and one p orbital to form an sp hybrid orbital. Two sp orbitals on an atom point in opposite directions and are the basis for molecules like acetylene (the gas used in old-time miners' carbide lamps), oxygen, and nitrogen.

You can also take one s orbital and two p orbitals to form sp2 orbitals which lie in a plane and form angles of 120 degrees.

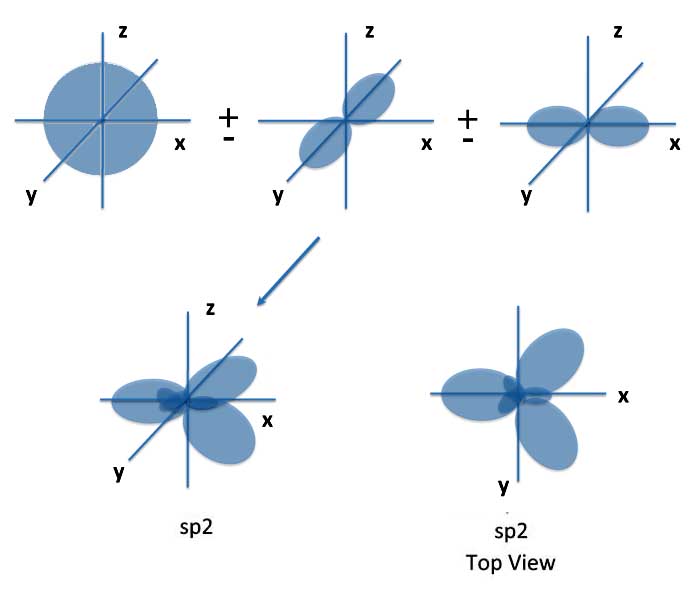
Some molecules with sp2 hybrid orbitals are formaldehyde, ethylene (used to make oranges ripen), and the famous (or infamous) benzene. And it was this last molecule that got Linus into his first of many controversies. That was the theory of resonance.

What is Resonance?

Anyone who has taken a beginning course in chemistry which has a section on organic molecules knows about resonance theory. What they may not know is that how controversial the theory has been - particularly since it is universally taught and plays a fundamental role in understanding molecular behavior.

But for Joe and Josephine Blow who haven't heard of resonance theory, we'll say that it is a way to represent molecular structures when a single picture doesn't do the job. But 'ere we proceed, a brief review of elementary middle school chemistry will be in order.

Molecules, as we repeat ad nauseum, are atoms held together in certain arrangements. The simplest molecule is hydrogen, H₂. You get a hydrogen molecule by two hydrogen atoms coming together.

H^. + ^.H → H:H

You'll remember that the two dots are two electrons, and electrons like to form pairs. When you get a pair of electrons between the two atoms - you get a chemical bond. Or more specifically a covalent chemical bond.

To simplify things, chemists prefer to draw bonds as lines.

H:H is the same as H-H

Sometimes you get more than two electrons between atoms. It's common to have four or even six. Carbon dioxide - the big baddie of global warming - has the structure:

:Ö::C::Ö:

Notice that not all electrons are between the atoms. These lone pairs are non-bonding electrons and don't help hold the atoms together. But they don't hurt either.

Now you can write this structure more succinctly by drawing a line for each pair of bonding electrons and not writing the lone pairs.

O=C=O

Some molecules have three electron pairs between the atoms. One example is carbon monoxide, the deadly gas that is given off by partial combustion of badly adjusted engines and furnaces and which at borderline lethal levels has made people think their houses are haunted.

:C:::O:

Or in simplifed form:

C≡O

Again we ignore the two pairs at the end of the molecule that aren't part of any bond.

Now there are all sorts of structures from the simple to the complex. But since carbon compounds are so common, there's even more abbreviations for them. You can just leave off the carbons and draw the bonds. And you can also leave off the hydrogens, realizing that the number of hydrogen atoms on typical organic molecules is found by subtracting the number of bonds on the carbon atom from 4.

For instance, let's take propane, the fuel that you see used in the shuttle vans in some state and national parks and which was made famous by the show King of the Hill. You have three carbon atoms and eight hydrogen atoms. And so we can draw it so that

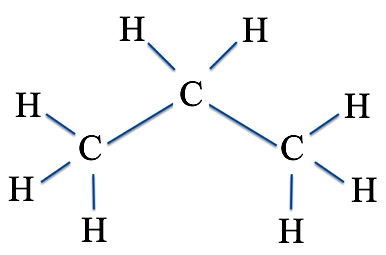      is the same as      

Another more complex molecule is butadiene, which is used in making rubber.

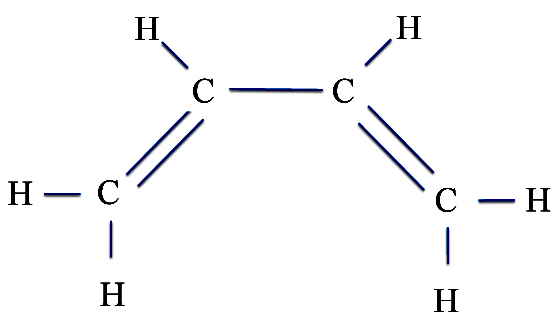      is the same as      

Now what we'll do is show how these diagrammatic structures are used in modern theory. But to avoid having you reply as Sidney Brand did when Captain Mephisto explained how the Secret Transforming Machine worked, we'll just stick just with the basics.

Remember we drew the hydrogen molecule as two H's with a line connecting them or as the two H's with two dots.

H:H       or       H-H

Let's consider this most famous - or as we said infamous of molecules

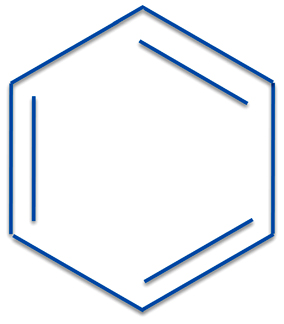
which is benzene. By the way, you may see a name of a chemical called "benzine". This is not an old or archaic spelling of benzene. It is a mixture of hydrocarbons, mostly pentane, hexane, and their isomers, and is similar to lighter fluid.

But regarding benzene, note what happens if you actually number the individual atoms. You can now draw the double bonds between different pairs.

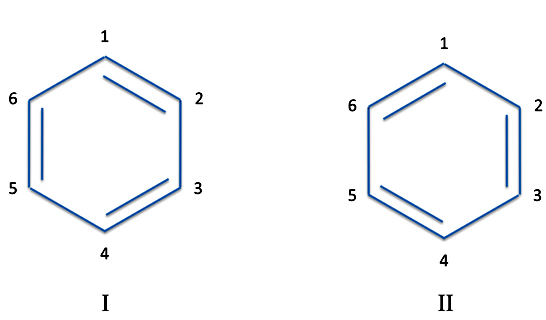
The two Structures I and II are what are called resonance structures. This is a most unfortunate choice of a word of which we have to blame on Werner Heisenberg, who we said was one of the originators of quantum theory. The word "resonance" tends to make us think the molecules are flipping back and forth between the two. This isn't the case. Instead the true structure is a combination or perhaps a superimposition of the individual structures. There are many molecules where the actual structure can't be represented in a nice single atom-and-bond drawing. Such molecules are called resonance hybrids of the individual structures.

Now curmudgeons will say Structures I and II are actually the same molecule. We've just flipped the molecule around. But that's not the case. Although the carbon atoms are indistinguishable experimentally, they are not the same atoms.

Now if benzene really had alternating double and single bonds, then the bonds wouldn't be the same length (double bonds are shorter than single bonds). In other words, benzene would not be a regular hexagon. But we know by various tests - chemical and spectroscopic - that it is. So there is quite literally something wrong with this picture.

But what really distinguishes benzene is that the six bonds don't react like your run-of-the-mill double bonds nor do they act like single bonds. Instead they act like, yes, a hybrid of the two.

So it is more accurate to represent benzene, not with single bonds and double bonds, but as having six one-and-a-half bonds. How to represent this unusual bonding was something chemists struggled with from the 19th century onward. The earliest chemists just didn't draw any bonds at all - they just represented benzene as a hexagon. But this representation violates our rules for making the abbreviated structures and is the way we now draw cyclohexane, C₆H₁₂.

More modern textbooks usually address the problem in a couple of ways. One is to draw both structures connected with a double arrow.

Resonance Hybrids of Benzene

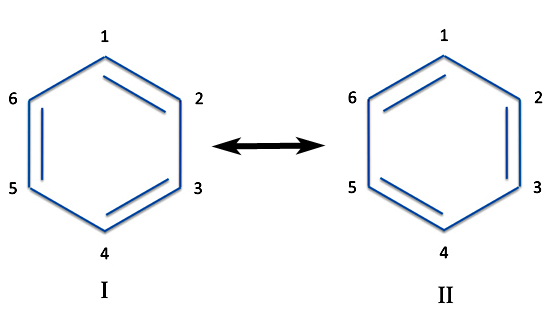
This representation, though, can be a bit unwieldy. So an alternative is to draw benzene with a circle on the inside. It would probably be best to write the circle as a dotted line (and sometimes it is) but more often people just draw a circle.

           

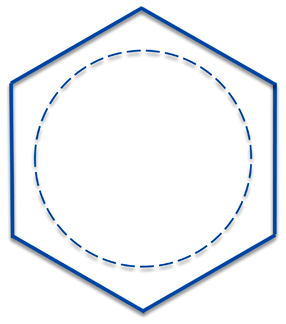
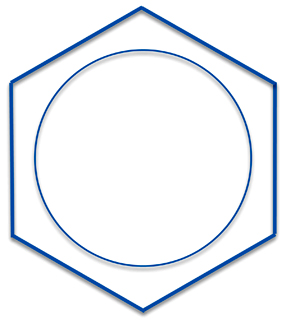
A problem with this circle-on-the-inside approach is that it really isn't useful when dealing with reaction analysis - sometimes discourteously referred to as "electron pushing". Instead you have to resort back to the classical three double and three single bonds representations to push your electrons correctly.

But Linus, rather than seeing benzene as a problem, saw it as an opportunity. This was a real test for the new quantum theory to show its mettle. So Linus adopted what is called valence bond theory which is a way to write the equation for the molecule in terms of individual bonds. Although it might seem this won't help for writing an equation for benzene, Linus showed - in one of the articles of his series on the chemical bond - it could be done. And this article is where he came up with resonance theory.

Valence Bond Theory: A Quantitative Resonance Theory?

To illustrate valence bond theory it's best to start off with the simplest molecule. That's, H₂. And for the hydrogen molecule, we we start off with the equations for the individual hydrogen atoms, each with its own electron.

s1(1) = A × e^{b × x1}

s2(2) = A × e^{b × x2}

All you need to know is that A and b are constants that are made up of other constants. The variable x1 and x2 is a reference to a location in space around the nucleus where the electrons from atoms 1 and 2 can be. And the e is the exponential function nowadays often represented as exp(x).

Now it is possible to represent the hydrogen bond as a simple product of the two orbitals. This wave function is written as.

Ψ(1,2) = s1(1)s2(2)

But since electrons are not physically distinguishable, it is better - for reasons we won't go into - to write what is called an "antisymmetrized" wave function. This is:

Ψ(1,2) = s1(1)s2(2) - s1(2)s2(1)

So in principle, if you know the math, you can actually use this equation to calculate properties of hydrogen.

But what if you have more than two atoms? For instance, let's go back to butadiene.

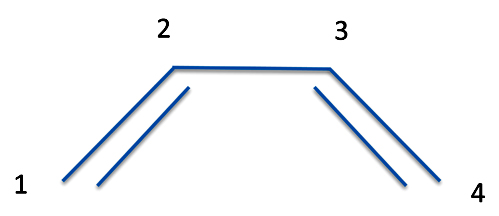
Now to simplify things we're going to only consider the bonds represented by the two detached lines. These are p orbitals from the carbon atoms and they can indeed be treated separately from the rest of the molecule. To show these aren't hydrogen atoms (but carbon) we'll label the atomic orbitals as p rather than s, and we can now represent the two bonds as:

P(1,2) = p1(1)p2(2) - p1(2)p2(1)

P(3,4) = p3(3)p4(4) - p3(4)p4(3)

But if we want to consider both bonds in a single equation, we have to multiply them together. So we get the wave function for the molecule, which we call Ψ, as

Ψ = [p1(1)p2(2) - p1(2)p2(1)][p3(3)p4(4) - p3(4)p4(3)]

So this equation represents the double bonds of butadiene.

(Note: Lest we arouse the ire of theoretical chemists and physicists, we realize that even this equation is a simplification. But if we try for more rigor, the equations rapidly get too unwieldy for teaching purposes.)

But now here is where things get interesting. Let's try to write a valence bond wave function for benzene. We begin by writing out the first resonance structure.

I

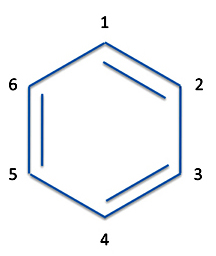
As in butadiene, we'll only consider the bonds formed by the p-orbitals. So we have three bonds which bond atoms 1 and 2, atoms 3 and 4, and atoms 5 and 6. This gives us three equations for the three bonds.

P(1,2) = p1(1)p2(2) - p1(2)p2(1)

P(3,4) = p3(3)p4(4) - p3(3)p4(4)

P(5,6) = p4(5)p6(6) - p5(6)p6(5)

The molecule - or at least these three bonds in the molecule - are written as:

Ψ_I = [p1(1)p2(2)-p1(2)p2(1)][p3(3)p4(4)-p3(4)p4(3)][p5(5)p6(6)-p5(6)p6(5)]

And we now have a wave function for one of the resonance structures of benzene.

But we also have structure II where the bonds are between atoms 1 and 6, atoms 2 and 3, and atoms 4 and 5.

I

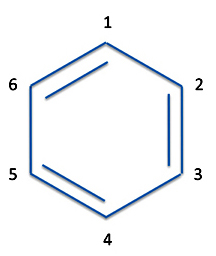
Of course, you can write the equations for the bonds in Structure II just as we did for Structure I.

P(1,2) = p2(1)p3(2) - p2(2)p3(1)

P(3,4) = p4(3)p5(4) - p4(3)p5(4)

P(5,6) = p6(5)p1(6) - p6(6)p1(5)

and we have for both Structures I and II:

Ψ_I = [p1(1)p2(2)-p1(2)p2(1)][p3(3)p4(4)-p3(4)p4(3)][p5(5)p6(6)-p5(6)p6(5)]

Ψ_II = [p1(1)p3(2)-p2(2)p3(1)][p4(3)p5(4)-p4(4)p5(3)][p6(5)p1(6)-p6(6)p1(5)]

Now we (again) remind ourselves the wavefunctions are actually mathematical equations that you could - if you wish - plot out or otherwise manipulate mathematically. So we can now combine the two wave functions, not as a product, but as a sum

Ψ_Benzene = Ψ_I + Ψ_II

which gives us a wave function for our resonance hybrid.

Now at this point, it seems like the work is done. But not quite. There are other resonance structures of benzene each with its own wave function. For instance, let's try this one:

Ψ_III = [p1(1)p4(2)-p4(2)p1(1)][p2(3)p3(4)-p3(4)p2(3)][p5(5)p6(6)-p6(6)p1(5)]

Once more a child - not of four, but let's say of six - can see that this wave function represents the rather oddball structure where a "bond" is formed across the ring from atoms 1 and 4.

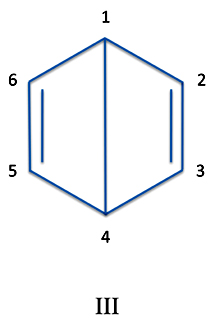
Of course, because the bond is so long it is actually quite weak and scarcely a real bond at all. But our structure is still a perfectly valid representation of an electronic configuration in the molecule.

(Note that if you were to distort the ring by bringing atoms 1 and 4 to within 0.00000000606 inches of each other a strong bond would form. This molecule has been synthesized and isolated. But it isn't benzene.)

Once more we see this structure is only one of a number of equivalents. There are two more of these so-called "Dewar" structures (named after the Scottish chemist of the nineteenth and early century, Sir James Dewar, who also invented the Dewar flask - that is, the thermos bottle).

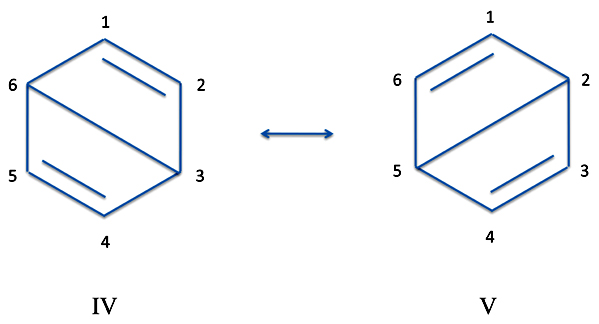
These structures clearly correspond to the wave functions:

Ψ_IV = [p1(1)p6(2)-p6(2)p1(1)][p2(3)p5(4)-p5(4)p2(3)][p3(5)p4(6)-p4(6)p3(5)]

Ψ_V = [p1(1)p2(2)-p2(2)p1(1)][p3(3)p6(4)-p6(4)p3(3)][p4(5)p5(6)-p5(6)p4(5)])

Now these wave functions - that is, the Dewar structures III, IV, and V - aren't as important as structures I and II. But they do contribute something. Moreover, each of these last three configuration does contribute the same amount as each other, however little that may be. So the new equation for benzene is a combination of the five separate functions but structures I and II are weighted differently than structures III, IV, and V.

Ψ_Benzene = c₁(Ψ_I + Ψ_II) + c₂(Ψ_III + Ψ_IV + Ψ_V)

The constants c1 and c2 are determined using calculus to where the energy of the combined wave functions is the lowest possible value. c₁ has a value of more than 99 % compared to c₂ - that is if we are talking about the ground state of the molecule. So when you get down to it, the first two structures represent benzene pretty well. Simple, no?

Well, no.

Linus's Competitors

For one thing, valence bond theory wasn't the only game in the quantum mechanical town. There was a competing method for making molecules. This was molecular orbital or MO theory which was developed by the American chemist and physicist Robert Mulliken. MO theory treated the electrons as if they were spread out over the entire molecule rather than being associated with particular pairs of atoms. Nor did it need to use hybridized orbitals.

Strangely, although MO theory doesn't specifically create chemical bonds, molecular orbital calculations were easier to do. For one thing, you didn't need to write the at times humongous numbers of separate resonance structures as a guide to the individual parts of the total VB wavefunction. Erich Hückel, a German physicist, was able to show in the early 1930's that you could explain benzene's chemical behavior using extremely simple MO calculations without having to write down any resonance structures. Erich's calculations were much simpler than Linus's VB treatment and was one of the first quantum mechanical calculations to explain why some compounds - called aromatic compounds - have the unexpected stability that puzzled chemists for decades. (If you have EXCEL with macro capability on your computer, you can do some calculations yourself if you just click here.)

Linus, though, stuck to his VB guns. Resonance theory, after all, was itself a simple embodiment of the quantum mechanical principles derived from valence bond theory. And quantitative MO calculations were still quite formidable even if they weren't as formidable as VB. Even after the computer era, MO calculations required specialized and often expensive software. They certainly could not be useful for a working chemist in an era where clunky mechanical desk top calculators were a luxury.

But with resonance theory you don't need mathematical calculations at all. Fortify a chemist with the general principles of chemistry and VB theory, and he has resonance theory, a powerful practical tool to use on a day-to-day basis.

Regrettably, some people didn't like resonance theory despite - or perhaps because of - the lack of mathematics and how easy it is to learn and use. The British chemist Michael J. S. Dewar was perhaps the severest of the critics. Although he acknowledged that valence bond calculations were a perfectly valid method for creating approximate wave functions, he disavowed any connection of resonance theory to VB wavefunctions.

In any case, resonance theory was too vague, and you can push electrons around as you like. Besides, resonance theory is all after the fact. Great for rationalizing experiments you've already run, but not a true predictive tool. And, Michael said, you could so use simple MO theory as a practical working tool for the bench chemist. This was possible using a modification of Erich Huckel's method.

Michael called the method - which he himself invented - the perturbational molecular orbital or PMO method. True, the PMO method did require some math, but these were the simplest back-of-the-envelope-paper-and-pencil calculations that even the most qualitatively minded chemist could use. Michael wrote the method up and published in it the Journal of the American Chemical Society almost exactly twenty years after Linus's papers. (For more detail on Michael and his method - which actually does work and certainly has some advantages over resonance theory - click here.)

Perhaps Michael's harshest criticism of resonance theory was it just wasn't anything new. It wasn't even invented even in America, for crying out loud! It was nothing more than a disguised form of the classical organic theory created by Sir Robert Robinson long - before quantum mechanics even existed!

(Honesty compels us to say that Sir Robert did not solely create the classical theory for today's organic chemists. Actually it was Sir Christopher Ingold that developed the terminology and conventions you read in modern organic textbooks. For his part, Sir Christopher readily adopted resonance theory and used it extensively in his own publications. You can read a bit more about the brouhaha that arose between Sirs Robert and Christopher if you click here.)

But one thing no one can deny is that valence bond calculations were considerably more difficult than those using molecular orbital theory. The advent of computers didn't change this fundamental fact. Even today if you buy a program for running quantum calculations on molecules, it's almost certainly an MO program. But a point to remember is that the equations we craft using either VB and MO theory are approximations, and the two methods are better called computational approaches rather than theories in the normal sense. As you add more and more rigor to the calculations, both techniques ultimately tend toward the same equations and so give us the same answers.

That doesn't mean you can't do VB calculations on a computer. And indeed once Moore's Law began kicking in, there was a resurgence in valence bond theory and new methods of calculations were developed that brought in elements of MO theory but kept the VB advantages. But the analogy of valence bond wavefunctions with the resonance structures is still strong and in VB articles in today's journals and (at times grotesquely overpriced) textbooks use resonance structures with considerable élan to represent the actual wavefunctions. It took a while, but we can say that Linus's theoretical ideas have been vindicated.

Later Life with Linus

Of course, not everything Linus championed has fared as well as his chemical theories. He has come under rather severe and at times strident criticism for his "orthomolecular" approach to health and medicine. This criticism particularly applies to his advocacy of Vitamin C.

Although it is true that about 40 milligrams a day of Vitamin C will prevent scurvey, it's also honest to say that virtually all of the scientific findings have not supported Linus's claim that taking gram quantities of Vitamin C is effective for preventing or curing other severe illnesses. Certainly most medical doctors do not accept that Vitamin C is an effective cancer treatment, and they can point to numerous clinical trials showing no effect.

But Linus, like all true believers, just would not accept any evidence to the contrary. So if a clinical trial showed there was no effect using Vitamin C in curing cancer, then he would simply say the doctors were also using other drugs that interfered with the Vitamin C. So is Linus saying to test Vitamin C you need to discontinue all other medications during the studies? However, medical ethics strongly prohibit keeping drugs with proven efficacy from patients in clinical trials. Also if properly designed, experiments should allow the researchers to identify drug interactions without denying patients potentially life saving medications.

However, Linus's advocacy and the fact his followers are as fervent as he has been responsible for the continued testing of Vitamin C as a therapeutic agent. And indeed some recent tests have shown it is possible to observe some anti-tumor activity using - not megadoses of Vitamin C - but mega megadoses and not when taken orally but when administered intravenously.

Does it work? Well, one paper reported cases where patients injected with Vitamin C supposedly survived much longer than usual. These patients had declined standard chemotherapy and opted for Vitamin C along with other non-traditional treatments. However, this paper was what is called a "best case" study, and which are often criticized since the investigators are in essence cherry picking favorable data out of a sea of information, much, if not most, of which might actually contradict the claims.

For instance, this study involved three - that's only three patients who got better. No effort was made to determine how many other people tried identical or similar Vitamin C treatments but did not have increased survival times. So it's impossible to determine if the recovery of the three patients was anything other than spontaneous remission - which sometimes does indeed happen even in advanced cancers - or if one of the other treatments was having a benefit. Even the authors said the tests did not prove that Vitamin C was the cause of the longer survival times.

Still, other research has suggested a beneficial effect with such huge dosages. But just how much Vitamin C is needed to see some anti-tumor effect? A lot - near the toxic levels (yes, too much Vitamin C can be toxic) - and at present is only possible in regulatory and physician supervised clinical trials. Also there was an in vitro test on cancer cells using the high levels of Vitamin C which are comparable to what you would get by intravenous injections. These tests showed reduction in tumor growth.

What seems to be happening is that at those concentrations, Vitamin C reacts to produce hydrogen peroxide in the cells and the peroxide may be preferentially attacking cancerous cells. But these findings are still a long way from Linus's claim that oral doses of gram quantities of Vitamin C would prevent or cure 75 % of all cancers. How he came up with these numbers and the claim is a mystery. Use of ultra high doses of injected Vitamin C is still a long way from being an actual therapy if it ever can be. The medical consensus is that Linus's claims are not correct.

Some people shake their head sadly about Linus, pointing out that what we are seeing is a perfect example of the Famous Scientist (Foul)-Up (FSFU for short). This is where once scientists have made names for themselves - particularly when fortified by a Nobel Prize - they not only accomplish little more of value for the rest of their lives but make darn fools of themselves. It seems that some experts, once they show the world they can provide a correct answer on one topic, then believe they are always correct on all topics. They begin blundering their way into fields of which they have no expertise, and they lose their ability to recognize and admit they were wrong.

But an FSFU need not occur long after the researchers prime years and it can indeed be in the field of their expertise. In 1951, Linus published his famous (and correct) paper on the structure of the alpha-helix of proteins. To solve the problem he used, not complex calculations, but what are now called Corey-Pauling space filling models. The models were just that - physical models created from wooden balls whose dimensions accurately represented the size of the atoms and the inter-atomic differences. Corey-Pauling models still have value in research although they are 1) now made out of plastic and 2) are increasingly supplanted by computer modeling.

Linus wasn't the only chemist working on the structure of proteins, of course. There was a group at Cambridge University in England that was every bit as active. But the two principles doing the research - John Kendrew and Max Perutz - although chemists and X-ray crystallographers - were not as versed in structural theory as Linus. They did not realize (as Linus did) that a crucial group of atoms in a protein, the amide linkage [-C(O)-NH-], had sp2 hybridization and were co-planar. Using the planar structure drastically reduced the number of possible shapes of the molecule. With a large data base of X-ray diffraction patterns and publications at hand and by fiddling with the models, Linus and his collaborators came up with the correct helical structure. The paper was published in 1952 in the (unrefereed) Proceedings of the National Academy of Sciences. Two years later Linus won the Nobel Prize in Chemistry for the discovery.

Fresh from this success, Linus decided to tackle the structure of DNA, the molecule that stores and transfers genetic information. At that time, about all that anyone knew about DNA is that it formed long fibers and that it was composed of long chains of "nucleotides" made up of sugar-and-phosphate molecules to which were attached one of four organic bases, adenine, thymine, guanine, and cytosine.

Again Linus constructed a model, and in February 1953 published a paper in the (still unrefereed) PNAS. The structure - a three-strand molecule (yes, three strands) with the sugar-and-phosphates on the inside - was completely and entirely wrong. Worse, there were chemical problems with Linus's molecule. DNA - that is, deoxyribonucleic acid - is as the name implies an acid with labile hydrogen atoms attached to phosphate groups. So when added to water, the molecule releases charged hydrogen atoms (protons) and making the water acidic. But Linus's proposed structure could not give up any hydrogen atoms without falling apart. In other words, Linus's nucleic acid was not an acid at all.

In fairness to Linus, he recognized that this was a weak point of his structure. But he had long recognized that a scientist might very well have found the more or less correct solution to a problem and yet held back publishing due to some minor discrepancy with the data. So he figured it was better to put his idea out on the table first and then worry about the details. Although the problem with his structure wasn't what we'd call a minor detail, it isn't quite fair to say - as some have - that Linus had "forgotten" freshman level chemistry.

At the same time two unknowns at the Cavendish Laboratory at Cambridge - Francis Crick, then an over-aged graduate student, who some say looked more like a racetrack tout than a crystallographer, and Jim Watson, a 24-year-old jug-eared former bird watcher from America who walked around with a goofy grin on his face - decided to try to solve the structure. Their strategy, Jim said, was to "imitate Pauling and beat him at his own game."

So they had the shop at the Cavendish make some (metal) models. Their first attempt was superficially similar to that of Linus, although they had built it before Linus's paper appeared. But the three strands of nucleotides were held together as a helix by magnesium or calcium ions not hydrogen bonds. Such a structure had the opposite problem as Linus's. What held the DNA molecule together before it was neutralized?

But Jim and Francis didn't see this as a problem and proudly called up Maurice Wilkins, who was the #1 authority on DNA in England and who was working at the Biophysics Research Unit at Kings College, London. The DNA project was becoming a major effort at Kings, and shortly before Jim arrived in Cambridge, John Randall, head of the BRU, had hired the crystallographer Rosalind Franklin also to work on DNA.

Now it seems that Maurice had believed that he would be in charge of the lab work and that Rosalind would be working for him. But Rosalind had understood that she had been hired to work independently, and the relationship between Maurice and Rosalind, which began as strained, deteriorated. But both Maurice and Rosalind (and Rosalind's student, Raymond Gosling) took the train to Cambridge to look at the model.

The meeting was a disaster. In a few brief words, Rosalind convincingly demolished Jim and Francis's structure. For one thing you couldn't hold the phosphate backbone together with calcium or magnesium ions. They would be surrounded by shells of water, and so their positive charge would be too dispersed to be links between negatively charged groups. Besides, the ions surrounded by water shells wouldn't fit into the model anyway. Also the proposed structure could not absorb the quantity of water the way DNA did. Such facile conversion between the low and high water forms required the phosphate backbones to be on the outside of the molecule where the water could move in and out easily. By the end of the meeting Jim noticed that the only ones talking about the model were him and Francis. Maurice, Rosalind, and Raymond went back to London.

Not surprisingly, an offer from Francis and Jim to officially join forces with Maurice and Rosalind was rebuffed. In fact, after he got back to London, Maurice wrote Francis a letter which more or less told him - politely to be sure - to stop muscling in on King College's research.

After hearing of the fiasco, Sir Lawrence Bragg, the head of the Cavendish, told his two problem children to knock off the nonsense. Maurice and Rosalind could work on the structure without having a couple of amateurs periodically dragging them up the Thames on 70 mile goose-chases to look at ridiculous tinker-toy-like constructions.

Francis, of course, had his thesis to complete and Jim decided to learn more about X-ray analysis by measuring the diffraction patterns of tobacco mosaic virus. Jim was able to prove that the virus in its crystalline form (yes, viruses can form crystals) had a helical structure. He managed to publish a paper on his work and so more or less convinced the fellowship board in America who approved his salary that he had not been totally wasting his time. Jim managed to get finances for another year at Cambridge.

Francis and Jim, though, kept working on DNA surreptitiously. Eventually, Maurice showed Jim a new X-ray picture of a DNA form discovered independently by himself and Rosalind and which clearly arose from a helical molecule. Also Maurice was convinced that Rosalind's data did confirm that the phosphate groups that formed the backbone of the individual strands were on the outside of the molecule.

Jim and Francis then had another crack at the structure (with the approval of Sir Lawrence and even acquiescence by Maurice) and two months after Linus's paper had appeared, they published their model in a short communication in Nature. Their structure was so good that it was accepted almost at once, and even Linus graciously conceded his error. Ironically, it was a former student of Linus's, Jerry Donahue, who had been sharing an office with Francis and Jim that gave them crucial knowledge to solve the structure. Jerry had pointed out to Jim that the textbooks that Francis and Jim were using gave the incorrect structures for two of the components of DNA, guanine and thymine. Jerry drew out the correct structures and Francis and Jim quickly nailed down DNA.

Jim and Francis, by the way, had asked Jerry if he wanted to be a co-author on their paper. No, Jerry said, his contribution wasn't enough to merit authorial status. They could just give him an acknowledgement at the end, which they did. Nine years later this paper would land Francis and Jim - but not Jerry - the Nobel Prize. Jim did, though, give Jerry part of their original model as a souvenir, a souvenir which ended up in the Franklin Institute in Philadelphia.

Some may argue that Linus's (incorrect) DNA structure was not a true FSFU. After all, he was working in an area of which he was probably the world's most qualified expert, and besides, just being wrong does not an FSFU make. But the DNA episode had some people thinking that with the success of the alpha-helix Linus began to completely adopt a theory driven approach to science where data is good as long as it confirms your theory and all other evidence is bad science. This might work sometimes, but can be very risky.

For instance Linus devised a theory of why inert gases, like xenon, act as general anesthetics. He thought they might form water complexes - essentially micro-ice crystals - in the brain that induce reversible unconsciousness. He knew the higher molecular weight gases would be the more polarizable (the electron "cloud" around the molecule can be pushed around and distorted) and so would better stabilize the "ice" in the brain. Then xenon should be a better anesthetic than neon which Linus knew was true.

Alas, try as he might, Linus and a number of his co-workers could not prove their case. Today the theory is almost universally regarded as wrong although Linus never seems to have given up hope.

Then there was the time ...

Well, we don't want anyone to think this is a trash-the-great-man type of essay. The Official CooperToons opinion is, yes, Linus was one of the most important scientists of the 20th century whose (correct) work is still important in both research and teaching.

Linus died in 1994 at age 93. Some have pointed out the irony that despite his taking the large doses of Vitamin C daily, he succumbed to cancer. But Linus himself said that his daily vitamin intake had delayed the onset by years, if not decades. Say what you like about Linus and his science and his politics, he was a very interesting character.

Appendix - The Schrödinger Equation for Beginners (Return to Essay)

We must emphasize that you cannot prove the Schrödinger equation. It is a physical law and like all physical laws is derived, either by reasoning, by observations, or both. Some textbooks just give it to you and say it is a postulate.

So what is this postulate? Well, if you write out the equation in full (and even this is a simplified version) you get:

-(h²/8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + V(x, y, z)ψ = Eψ

Now admittedly, this is one heck of a postulate. Particularly since postulates, according to Euclid, are supposed to be so fundamental and self-evident that they need no proof. This equation may be fundamental, but self-evident it isn't.

But what we can do is show, not how to prove the equation, but how to derive it from more familiar and simpler ideas. And it's surprisingly easy to do this if we go back and see what Erwin was actually doing.

One story is that one of the senior professors at Erwin's university chided him that he wasn't doing anything important at present. Well, since Erwin wasn't busy, how about giving a lecture on what was then a hot topic? That was the thesis that the French physicist, the Count Louis de Broglie, had written that predicted that electrons and other subatomic particles actually had a wavelength like light. Erwin gave the lecture, but the professor dismissed there being any wave nature of electrons since there was no wave equation for them.

Well, if you needed a wave equation, Erwin decided he'd make one. He began to reason something like this.

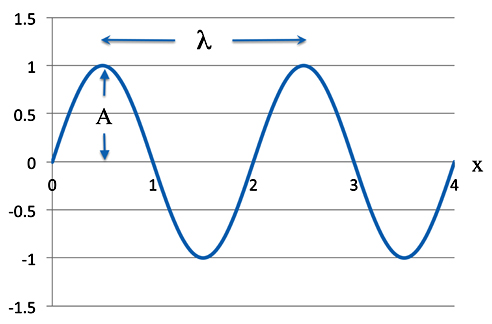
Take the classic equation for a wave. This is a nice simple sine wave.

ψ = Asin(2πx/λ)

As we know A is the amplitude - how high the wave is - and λ (the Greek letter lambda) - is the wavelength. Of course π is our old friend 3.1415926, etc., etc. The variable x is a position along the wave.

Well, Erwin said, let's first take the derivative of the wave with respect to position just like you did in middle school calculus (well, all right, high school calculus).

dψ/dx = Acos(2πx/λ) × 2π/λ

Since that was so much fun, Erwin did it again.

d²ψ/dx² = -Asin(2πx/λ) × 2π/λ × 2π/λ

Now group the various parts together.

d²ψ/dx² = -4π²/λ²Asin(2πx/λ)

At this point you'll notice that there's part of the equation that is just the original equation for the wave.

d²ψ/dx² = -4π²/λ²Asin(2πx/λ)

But since our sine equation was written as:

ψ = Asin(2πx/λ)

We can now write everything more succinctly.

d²ψ/dx² = -4π²/λ² × ψ

This is indeed a wave equation, a second order differential equation in fact. But at this point, there is nothing really new. Wave equations have been around as long as there has been calculus and waves.

But remember Erwin had given a lecture on the discovery of Count Louis de Broglie. Count Louis had found that electrons - which everyone thought of as particles - also had a wavelength like light. The way Count Louis deduced electrons had wavelengths was as simple as it was slick.

First Louis remembered what Einstein found about energy:

E = mc²

But he also knew that the German physicist Max Planck had found that light waves came in little packets of energy that Max called quanta, although we now call them photons. The energy of each photon was related to the frequency of the light - that is the cycles per second - which we label as the Greek letter nu, ν.

E = hν

And h is the constant we mentioned earlier called Planck's constant.

Since ν is the frequency of the light, we can rewrite the equation for photons in terms of the wavelength which is the λ in our wave.

E = hc/λ

where c is the speed of light.

But both mc² and hc/λ represent the energy of the light and are equal. So we can write:

hc/λ = mc²

And with a bit of algebra we end up with:

h/λ = mc

λ = h/mc

But unfortunately, you'll remember that we are writing the equation for electrons. And electrons don't travel at the speed of light. So we have to replace the constant c with the more mundane variable v which just means the velocity of the electrons.

λ = h/mv

Which is the aptly named De Broglie Equation.

At this point Erwin realized you could take the wave equation:

d²ψ/dx² = -4π²/λ² × ψ

And substitute Count Louis's equation for wavelength - that is h/mv - for λ.

d²ψ/dx² = -4π²/(h/mv)² × ψ

Now with some middle school algebraic gymnastics:

d²ψ/dx² = -4π²m²v²/h² × ψ

d²ψ/dx² = -4π²m(mv²)/h² × ψ

d²ψ/dx² = -8π²m(½mv²)/h² × ψ

Now note that at one point we have the expression ½mv² in the equation.

d²ψ/dx² = -8π²m(½mv²)/h² × ψ

Again from middle school you'll remember this is the equation for kinetic energy which physicists like to represent using T.

T = ½mv²

(T is probably an abbreviation of the French travail mécanique or quantité de travail but no one's really sure.)

So put the T into the equation and perform some more algebra:

d²ψ/dx² = -8π²mT/h² × ψ

-(h²/8π²m)d²ψ/dx² = Tψ

At this point we have to remember (again) that the total energy of a system is the sum of the kinetic and potential energy.

E = Kinetic Energy + Potential Energy

which we represent as:

E = T + V(x)

The x in the V(x) is to show that potential energy is a function of the position of the electron.

We now rewrite our last equation as:

T = E - V(x)

We can now substitute the expression E - V(x) for T in our wave equation and get:

-(h²/8π²m)d²ψ/dx² = [E - V(x)]ψ

Which with more algebra gives us:

-(h²/8π²m)d²ψ/dx² + V(x)ψ = Eψ

And believe it or not we have the Schrödinger equation in one dimension.

At this point, you can calculate energies and positions of electrons as long as they stay on a straight line. But if you want to calculate how electrons behave in space, we need to go to three dimensions.

Which is actually pretty easy. Just add in the y and z coordinates like we have for the x coordinate and substitute the partial differential sign, ∂, for the single variable differential, d.

-(h²/8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + V(x, y, z)ψ = Eψ

Hey, presto! The time indepdendent Schrödinger equation in three dimensions!

Now admittedly this is a pretty long expression. And when writing textbooks, the authors like to save space. We can do this by coming up with some abbreviations for the more long-winded notation.

So we start off with our last equation which is:

-(h²/8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + V(x, y, z)ψ = Eψ

Now the conventions of calculus let us rewrite this as:

-(h²/8π²m)(∂²/∂x² + ∂²/∂y² + ∂²/∂z²)ψ + V(x, y, z)ψ = Eψ

Which means we have defined an operator as:

∂²/∂x² + ∂²/∂y² + ∂²/∂z²

That is, we understand that if you write this expression in front of a function it means to take the second derivative with respect to the position of the electron coordinates x, y, and z.

Let's simplify things further by defining the symbol ∇² as:

∇² = ∂²/∂x² + ∂²/∂y² + ∂²/∂z²

And we now have:

-(h²/8π²m)∇²ψ + V(x, y, z)ψ = Eψ

Or equivalently

-(h²/8π²m)(∇² + V[x, y, z])ψ = Eψ

And if we can abbreviate further with:

∇² + V[x, y, z] = H

where H is the famous Hamiltonian operator. So after all this we now have the Schrödinger equation as:

Hψ = Eψ

Now that's a self-evident postulate!

(Return to Essay)

 

References

Linus Pauling: A Life in Science and Politics, Ted Goertzel and Ben Goertzel, Basic Books, 1995

"The Nature of the Chemical Bond. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules", Linus Pauling, Journal of the American Chemical Society, Vol. 53, Issue 4, pp. 1367-1400, 1931

Brilliant Blunders: From Darwin to Einstein - Colossal Mistakes by Great Scientists, Mario Livio, Simon and Schuster, 2013. Perhaps one of the most interesting chapters is on making it rain by cloud seeding. This was a case where the process worked in lab without a doubt and yet to this day has not been shown to really, really work - as they say in the commercials - in the real wide world.

The Double Helix: A Personal Account Of The Discovery Of The Structure Of DNA, James D. Watson, Atheneum, 1968.

Linus Pauling Online, Oregon State University, http://pauling.library.oregonstate.edu/

The Race for DNA, Oregon State University, http://scarc.library.oregonstate.edu/coll/pauling/dna/index.html

"The Turn of the Screw: James Watson on The Double Helix and his changing view of Rosalind Franklin", Maggie Koerth-Baker, http://boingboing.net/2012/11/08/the-turn-of-the-screw-james-w.html

"Robert Robinson - 13 September 1886 - 8 February 1975", Biographical Memoirs of Fellows of the Royal Society, Alexander, Lord Todd and John W. Cornforth, Vol. 22, pp 414-527, 1976.

"Electronic Theories in Organic Chemistry" The Great Soviet Encyclopedia, 1979.

"From Chemical Philosophy to Theoretical Chemistry: Dynamics of Matter and Dynamics of Disciplines, 1800-1950", Mary Jo Nye, University of California Press (1994)

Advanced Organic Chemistry, Frederick March, Wiley, 2007.

Linus Pauling: Crank or Genius, Accuracy in Media, 1994, posited at http://www.math.buffalo.edu/mad/physics/Bransonrobbed.pdf. The original report is - to be honest - from what is oft called a "conservative watchdog" which ended up with a footnote urging people to sending an enclosed card to the New York Times to stop the "kid glove" handling of leftist radicals. I think we must consider this an vehemently anti-Linus article. The topic of Dr. Branson's contribution (at least) to the alpha-helix is dealt with in other articles as well, some of which are laudatory to Linus.

Vitamin C megadoses have been studied quite a bit in clinical trials for various maladies, and you get mostly the conclusions there's no effect in most cases (although Vitamin C does prevent and cure scurvy). What confuses people is that when you have a multitude of tests run by many researchers and over decades, in some of the tests you might see benefits, at other times negative effects, and in other tests no effects at all. Although this is a somewhat oversimplifed statement, generally when you have studies showing such confusing and contradictory results, you're usually looking at something that has no effect.

"Intravenously administered vitamin C as cancer therapy: three cases", Canadian Medical Association Journal, Sebastian J. Padayatty, Hugh D. Riordan, Stephen M. Hewitt, Arie Katz, L. John Hoffer, Mark Levine, March 28, 2006 vol. 174 no. 7 doi: 10.1503/cmaj.050346

"Pharmacologic doses of ascorbate act as a prooxidant and decrease growth of aggressive tumor xenografts in mice", Qi Chen, Michael Graham Espey*, Andrew Y. Sun, Chaya Pooput, Kenneth L. Kirk, Murali C. Krishna, Deena Beneda Khosh, Jeanne Drisko, and Mark Levine, Proceedings of the National Academy of Sciences, Vol. 105, Issue 32, pp. 11105–11109, (2008).

"Pharmacologic ascorbic acid concentrations selectively kill cancer cells: Action as a pro-drug to deliver hydrogen peroxide to tissues", Qi Chen, Michael Graham Espey, Murali C. Krishna, James B. Mitchell, Christopher P. Corpe, Garry R. Buettner, Emily Shacter, and Mark Levine, Proceedings of the National Academy of Sciences, Volume 102, Issue 38, pp. 13604–13609, (2005).

"High dose vitamin C and cancer: Has Linus Pauling been vindicated?", David Gorski, http://www.sciencebasedmedicine.org/high-dose-vitamin-c-and-cancer-has-linus-pauling-been-vindicated/

"Vitamin C: Fact Sheet for Health Professionals", National Institutes of Health Office of Dietary Supplements, http://ods.od.nih.gov/factsheets/VitaminC-HealthProfessional/

"Kinetic Energy", Physics Hypertextbook, http://physics.info/energy-kinetic/