
James and Pythagoras: Did Jimmy really do it better?
Everyone, that means everyone, knows about the Pythagorean theorem. That's the theorem that says for a right triangle the sum of the squares of the hypotenuse is equal to the sums of the squares of the other two sides. The theorem has been known for thousands of years and well before Pythagoras was born.
That is, the theorem was known. The proof wasn't formulated until later. The Egyptians knew that a triangle with dimensions 3 X 4 X 5 formed a 90 degree angle, and they used this knowledge to lay out right angles of buildings, temples, and pyramids. The Chinese have diagrams that show they knew the general idea but didn't give a rigorous step-by-step demonstration de rigueur by today's math teachers.
But the first known real proof, in the modern sense, is in Euclid's Elements. Euclid's proof is rather long and requires slapping three squares on the side of a right triangle and then divvying it up in a number of non-obvious ways. As simple as the actual equation is, not too many people can figure out a proof on their own. Also if you do learn it and later try to remember it, you generally have to delve back into the textbooks.
But there is one proof that once learned is pretty easy to remember. That's a proof devised none other than James A. Garfield. Yes, that's the James A. Garfield, the American President. However, he wasn't president when he thought up the proof. He was just a congressman from Ohio, and the proof was published in the New England Journal of Education in 1876. If you learn Jimmie's proof, and understand the logic behind it, then you'll probably remember it.
Of course, to prove a theorem about a right triangle, you need a right triangle. Since this is a proof applying to all right triangles, we specify the lengths of the sides by letters not by any specific numbers.
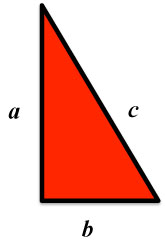
Figure 1: Jimmy's Triangle
So now we can specify exactly what we want to prove.
a2 + b2 = c2
All right. The first step in Jimmy's proof is to make a copy of the triangle and place the two triangles top-point-to-right-point.
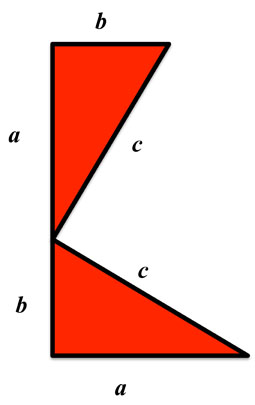
Figure 2: Two Triangles
Finally we connect the two other corners. This generates 1) another triangle (in blue) and a combination of all the triangles to form a trapezoid.
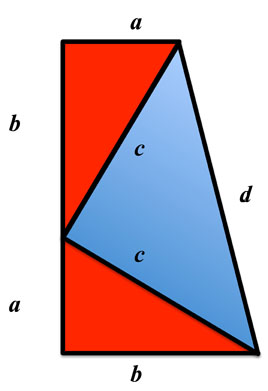
Figure 3: Jimmy's Trapezoid
Now it is possible to show that the blue triangle is also a right triangle (although it looks like a right triangle, we have not proven it). Well, you'll remember that the angles in a triangle sum up to 180 degrees. So a right triangle has one 90 degree angle (the one we call γ). So the two other angles must sum to 90 degrees.
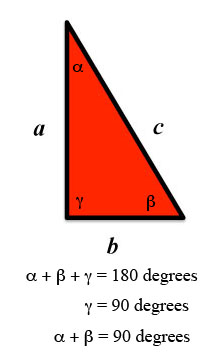
Figure 4: The Angles
Note that to form the trapezoid, we have to make sure that when we join the two original triangles, they form a left hand edge that is a straight line. The angles that touch are α and β. These, we note add to 90 degrees. Since the sum of angles that make up a straight line also equal 180 degrees, the left corner angle of the blue triangle has to be 90 degrees as well. Ergo, our blue triangle must be a right triangle as well.
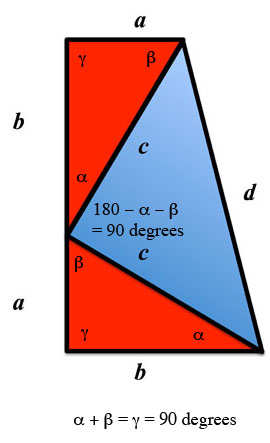
Figure 5: Calculating the angle.
So our trapezoid is formed by three right triangles, the two original triangles and the new one, which is also an isosceles triangle, ergo, a triangle where two sides are of equal length.
Now like the $200 an hour psychiatrist said after six weeks of treatments, now we can begin, yes?
Proof
The first step of Jimmy's proof is to realize you can calculate the area of the trapezoid by just summing up the areas of the individual triangles. As we all know from our school days, a triangle's area is equal to half the base times the height.
Area = ½ base × height
The base and height of our original triangles can be either a or b. So for one of the (red) triangles, the area then is simply
Area = ½ a × b
Note sides c were the hypotenuses (hypotenusi?) of our original triangles. But they form the new (blue) right triangle which has the hypotenuse d. But we don't need to know the hypotenuse length to calculate the new triangle's area, just the base and height. For the blue triangle, the base and height have the same length and are equal to c. So the area of the new (blue) triangle is
Area = ½ c × c = ½ c2
With two red triangles and the one blue triangle, we know that the total area of the trapezoid is equal to
Area (Trapezoid) = 2 × Area of Red Triangles + Area of Blue Triangle
which if we substitute the specific sides of our figure becomes
Area (Trapezoid) = 2 × (½ ab) + ½ c2
or
Area (Trapezoid) = = ab + ½ c2
Or twice the area is equal to
2 × Area (Trapezoid) = 2 × ab + c2
Now at this point, we back up and note that there is another way to calculate the area of a trapezoid. It is simply one-half times the sum of the two bases multiplied by the height. We won't prove this here, but it is a well known theorem.
Area (Trapezoid) = ½ (b2 + b1) × h
For the trapezoid we created, one of the bases is side a and the other base is side b. So the sum of the two bases is simply a + b. But coincidentally, note that the height of our particular trapezoid is also a + b. So the total area of the trapezoid can be written as:
Area (Trapezoid) = ½ (a + b) × (a + b)
Now here requires quite formidable middle school algebra. You have to expand the formula.
Area (Trapezoid) = ½a2 + 2(½ab) + ½b2
= ½a2 + ab + ½b2
Or twice the area is
2 × Area (Trapezoid) = a2 + 2 × ab + b2
Now if you'll look back further up the page, we had already calculated a formula for twice the area.
2 × Area (Trapezoid) = 2 × ab + c2
So we can equate the two equations.
a2 + 2 × ab + b2 = 2 × ab + c2
The 2 × ab on each side of the equation cancel out and - hey, presto! - we get
a2 + b2 = c2
So Jimmy knew what he was doing.
How about that?
The Presidential Proof of the Pythagorean Theorem (or the PPPT) is, as we said, pretty simple if you understand middle school geometry. But it has been noted by some mathematicians that Jimmy's proof - as simple as it is - is by no means the simplest. Furthermore people who like to trash American politicians can point out that the PPPT can be seen as nothing more than a needless complication of the Chinese proof we alluded to.
The Chinese proof was proposed long before modern algebraic techniques were developed by Islamic mathematicians. So it is not completely clear exactly what the proof was. But there is a modern version that is based on the ancient Chinese diagrams and uses only the most rudimentary algebra.
If you take Jimmy's diagram, you can find that you can double it and create a square surrounded by four identical right triangles (by clicking the image below, you can expand the image to a separate - and wide - window). This produces the diagram the Chinese used as their proof. That is we now have two squares, one inside the other. The big square is formed from the four red triangles and the smaller inside blue square.
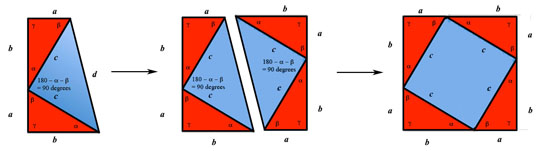
Figure 6: Is Jimmy's American Proof Really Chinese?
Now the area of the big square is equal to four of the red triangles plus the blue square..
Area (Big Square) = 4 × Area Red Triangle + Area Small (Blue) Square
If you substitute the equations for the areas of the triangles and the square you get
Area (Big Square) = 4 × (½ ab) + c2
This simplifies to
Area (Big Square) = 4 × (½ ab) + c2
= 2ab + c2
Now note that the length of the sides of the big square is equal to the sum of the sides of the red trianges, which is a + b. That means that the area of the big sqaure is also equal to:
Area (Big Square) = (a + b)2
This can be expanded to:
Area (Big Square) = a2 + b2 + 2ab
So we now have two equations for the area of the big square which we can set equal to each other
a2 + b2 + 2ab = 2ab + c2
So once more you cancel out the 2ab and you get
a2 + b2 = c2
With this proof all you need to know is the how to calculate the area of a triangle and the area of a square. Certainly simpler than Jimmy's proof.
There is some indication that the Pythagorean theorem was more widespread than previously believed. If one tradition is true, then the theorem was known in prehistorical North America, and there were trans-Atlantic trading routes established far longer ago than previously believed.
In any case, in at least one Native American legend there is the tale that a chief practiced polygamy. He had one principal wife and two secondary wives. The two secondary wives and their infants slept on robes made of buffalo hide. The principal wife with her child slept on a bed made from a hippopotamus hide. Naturally because of the rarity of the hippopotamus hide - which had to be imported from Africa - the status of the son of the principal wife was equal to the status of the two secondary wives put together.
And what does this prove about the inhabitants of prehistoric America?
It shows they knew that sons of the squaw on the hippopotamus was equal to the sons of the squaws on the other two hides.
Return to CooperToons Department of Education