Johnny - He invented it.

Game Theory at the Little Bighorn

A Most Merry and Illustrated Introduction, Sort Of

Everybody has heard of Game Theory. This is the discipline that was invented in the 1930's by the Hungarian mathematician (and later naturalized US citizen) Johnny Von Neumann. Game theory is a way of analyzing virtually everything you do when you do it with someone else.

Not that it's above criticism. Even today with Nobel Prize winning game theorists being portrayed in hit movies, you'll read stuff like:

Game theorists are often viewed as precocious children who wander in wide-eyed innocence expecting that their toy weapons will slay live dragons as well as they did inanimate ones.

Initially there was a naive-bandwagon feeling that game theory solved innumerable problems. That has not turned out to be the case.

Game theory is no doubt wonderful for telling stories. However, it flunks the main test of any scientific theory: The ability to make empirically testable predictions. In most real-life situations, many different outcomes - from full cooperation to near-disastrous conflict - are consistent with the game-theory version of rationality.

Perhaps these judgements are a bit severe. As we'll see, game theory is more of a computational or programming technique than an actual theory per se. So blaming game theory for failed predictions seems akin to blaming FORTRAN because you got the wrong answer.

As to what rational means to a game theorist, we'll see it's not necessarily the meaning of normal everyday conversation. Certainly in the fairly simple examples we use here, a rational decision is one where we avoid the worst possible situation. This is what leads to the occasionally odd-ball finding - such as the famous Prisoner's Dilemma where the most rational decisions actually produce a less positive outcome for all the individuals than an alternative choice. But essentially a rational choice is one where things won't get worse for a player regardless of what the other players decides.

Perhaps we can make this clear if we apply game theory to a most interesting problem. That is the problem of what to do at:

The Battle of the Little Bighorn

The First Part

Or rather, what should Marcus Reno have done?

In brief, the Battle of the Little Bighorn began because General Phillip Sherman sent General Alfred Terry to get the Native Americans who had left the reservations in the Spring of 1876 back on the reservations. Alfred in turn had sent his famous but somewhat controversial subordinate, Lieutenant Colonel George Armstrong Custer, to look for the Indians down the Rosebud River.

Alfred's instructions - which gave George leeway to depart from them if George "saw sufficient reason for doing so" - were to go south from the mouth of the Rosebud to it's headwaters. But even if he found the Indian trail - that is the marks on the ground of the horses hooves and the travois - Alfred would like George to keep going south even as far as the beginning of the Tongue River. Then if he sees no Indians he should turn west until he reaches the Little Bighorn and move north along the river. Alfred would be coming south along the Bighorn and he and George should trap the Indians between them.

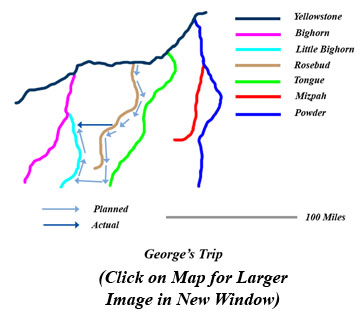
But George turned west as soon as he saw the Indian trail. This was long before the headwaters of either the Rosebud or the Tongue River. Then with the help of Crow scouts George located the village camped a little south of where the Little Bighorn River joins the Bighorn.

About 1:00 in the afternoon (local time) of June 25, 1876, George divided his command. He sent the cantankerous Captain Frederick Benteen to check if there were Indians to the west and south. He then ordered Major Marcus Reno to attack the village by charging north along the floodplains of the river. George told Marcus to attack and he - that is George - and "the whole outfit" would support him.

So we will now assume Marcus, and the Indians have read introductory game theory texts. They now apply the theory - which we mentioned is actually more of a computational technique rather than a theory - and decide what to do.

Marcus now has some choices to make.

First he can ignore George's order.

Or he can do as ordered and attack.

Of course there are the Indians. They also have options. Once they see the attack coming:

They can flee and scatter with their families.

They can counterattack.

To use game theory, we now have to rank the consequences of the actions. This requires objectivity in a qualitative and quantitative sense. But we'll give it a go.

For Marcus the worst thing that can happen to him is to disobey a direct order and not attack. Bad! Bad! Bad!

And what's really bad is if Marcus retreats and the Indians retreat as well. Marcus disobeys a direct order and the Indians get away. For Marcus this outcome and what game theorists call the Expected Utility of this outcome is -100.

But for the Indians, this "strategy" - that is, Marcus doesn't attack, and they flee - is the best thing. Why? Well, Marcus runs away, and the Indians get away with their families. So the Expected Utility for the Indians here is +100.

But what if Marcus doesn't attack and the warriors charge? If the Indians took after him, then maybe Marcus won't look quite as bad. But it's still pretty bad. So we'll rank this outcome as a -90.

For the warriors, this strategy also has a bit of a penalty. They are able to enter into battle - an activity of honor for the native warriors - but they will loose ability to protect their families as they attempt to flee. But certainly the Indians have the advantage. So we'll rank this outcome for the Indians as a +75.

The best for Marcus, though is he can attack and the Indians flee. Then Marcus will be following his orders and the Indians will not have time to break camp. He will be completely successful. So we give him +100.

For the Indians this is terrible. Some warriors could get away but almost all others Indians - particularly the women and children - will be killed or captured. We'll rate this as -100 for the Indians.

On the other hand suppose Marcus attacks and the Indians charge. Then Marcus will be following his orders but will also be fighting the warriors. But engaging in battle is something he, as a soldier, is familiar with. So for this we'll give Marcus a bit of a positive number, +25.

As for the warriors who are attacking, they will be able to gain prestige by killing opponents and counting coup. But they will also suffer casualties. It's a bit more positive than for Marcus, so for this we'll give the warriors a +50.

So what do we do now? Well, it's customary to organize game theory problems into tables like this one:

The Expected Utilities - the "payoffs" - for Marcus are the first numbers in the boxes and those for the Indians are the second numbers. So if Marcus attacks and the Indians charge Marcus is awarded a 25 and the Indians 50.

The question now is what should everyone do?

Usually the first thing to do is look at "Player 1" - in this case Marcus - and at his payoff values. If one of his strategies has values in one row that are both above his values in another, then the strategy with higher values is said to strictly dominate the other which in turn is said to be strictly dominated by the first.

Since 25 (Attack) > -90 (Don't Attack) and 100 (Attack) > -100 (Don't Attack), then Marcus's strategy of Attack does indeed strictly dominate his strategy of "Don't Attack". Or equivalently, "Don't Attack" is strictly dominated by "Attack".

Rule #1 in game theory:

Never play a strictly dominated strategy.

Which means:

Marcus should attack!

Which is exactly what he really did.

And the Indians?

Note that there is no strictly dominated strategy for the Indians. 50 (Charge) > -100 (Flee) but 75 (Charge) < 100 (Flee). If there was a strictly dominated strategy, they would discard it for the strictly dominant strategy. But they can't do that.

But the Indians can look at what Marcus is going to do. The warriors - knowing game theory - realize that Marcus will follow his strictly dominant strategy and will attack. So in that case, since 50 (Charge) > -100 (Flee), we know:

The warriors should attack!

Which is what they did.

So to summarize our analysis of the first part of the battle, Marcus realizes he should always attack as that is the strictly dominant strategy.

The Indians, though, do not have a strictly dominant strategy. But they realize Marcus will always attack. So their best option is for them to attack as well.

And in the actual battle Marcus and the Indians did what game theory says. That is, they both attacked and so took the most rational approach.

Plus Ça Change

Now part of the criticism of game theory is that the assigning of the Expected Utilities - the "payoffs" - is a bit iffy. And changing the payoffs can make a big difference in what is the "rational strategy".

For instance, suppose Marcus believed that if both he and Indians attacked, he would be wiped out. But if he retreated he could at least get away. So <attack, charge> would be the worst thing that would happen. So we'll give that a -100.

But now <attack, flee> is the best. So that becomes 100. We'll keep <don't attack, flee> as -90 and make <don't attack, flee> to be 25.

So the modified table is

Note that now there are no strictly dominated strategies here. True, there are ways to handle such games. One - which we won't bother with details - is to alternate strategies with a certain probability. In this case the best strategy is that Marcus should not attack 86 % of the time and the Indians should charge 88 % of the time. This doesn't, of course, help much if you only have one chance to attack or not attack.

However, the tables are not really representing exactly what happened. Game theory tables are most suitable when neither participant knows what the other has done or they perform their strategies at the same time. This is clearly not the case at the Little Bighorn.

Instead we should make a game tree where the sequential nature of the actions are taken into account. You start off with Marcus - who makes the first decision - at the top, and move down with the Indians deciding what to do next. Then you put the Expected Utilities at the bottom.

So the game tree for Marcus's Modified Attack is:

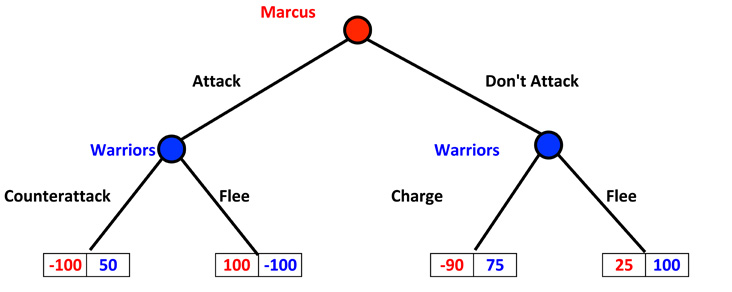
Game Tree: Marcus's Modified Attack

To find the best approach you work backwards and wipe out the worst cases.

First look what happens if Marcus has attacked. The warriors can either counter attack - which is rated 50 - or flee - which is rated as -100. So definitely the warriors will charge if Marcus attacks. So we wipe out the worst case.

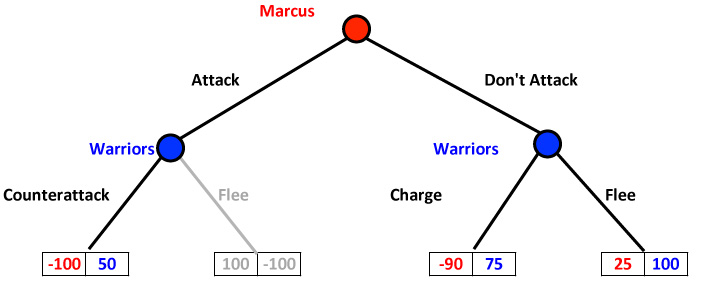
Game Tree: Marcus's Modified Attack

OK. What if Marcus doesn't attack? Then if the warriors charge, they get a 75. If they flee they get a 100. So if Marcus doesn't attack, the warriors will flee. So we wipe out the warriors' "charge" option.

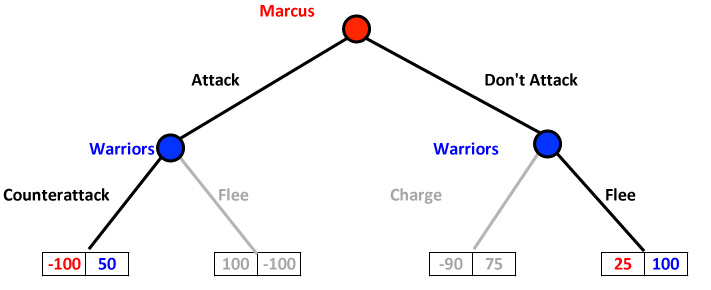
Game Tree: Marcus's Modified Attack

So what will Marcus do? Well, he knows game theory too. So he can follow our reasoning and knows that if he attacks, the warriors will charge - giving him the worst case -100 - or he can decide to not attack. He also knows if he doesn't attack, the worst case for the Indians is to charge. So they will flee, leaving him with an OK Expected Utility of 25. So once more knocking out the worst case, we see that Marcus realizes his best course - or at least his most rational course - is to not attack.

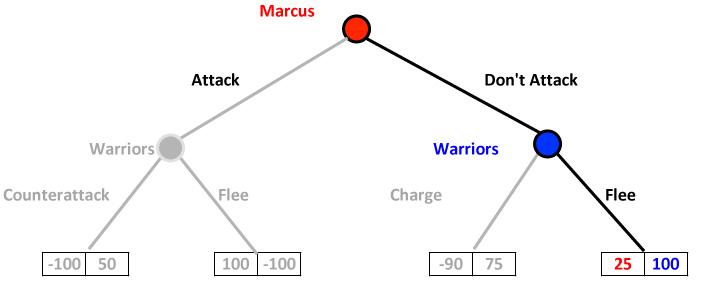
Game Tree: Marcus's Modified Attack

So if Marcus believes he will be wiped out if the Indians attack, then he should not attack and the Indians will flee.

And George will be really ticked off.

But we mentioned that what really happened was Marcus attacked and the Indians counterattacked. So clearly he did not believe he would be wiped out if the warriors counterattacked.

Remember that the Expected Utilities are added by considering the relative advantage offered to the individual participant. The absolute numbers don't matter. Also the Utilities for one player don't play into the ultility of the other. So in practice it really isn't too hard to assign objective utilities to historical events - even if you know the outcome.

What Happened Next: Marcus Skirmishes.

What Happened Next

As the warriors came out of the village, Marcus and his troops continued to advance. Now because warriors preferred hit-and-run tactics, Marcus and other soldiers were surprised when Indians counterattacked. If fact, it had become accepted wisdom that if you attacked a band of Indians, they would run. But that wasn't always the case by any means.

Also the fact that Marcus started his attack about two miles from the lower end of the village gave the warriors time to get their horses. So by the time Marcus got within a few hundred yards of the lodges (i. .e, the teepees) - to quote Marcus's official report - "at the same time the very earth seemed to grow Indians." So Marcus was reaching a new decision point.

It's important to remember that George had told Marcus to attack and - we have to emphasize this - then "the whole outfit" would support him. Now supporting of an attack usually means following immediately behind the first wave or making a coordinated side attack. It does not mean riding over high terrain for about an hour looking for a place to cross a river. Which is what George actually did.

But Marcus launched his attack, was counterattacked in return, and saw no support from George.

OK. So what should Marcus do now?

Well, once more let's look at the options.

First he can continue his attack and try to ride into the village.

He can dismount and wait for the promised support.

Of course there are the Indians. They also have new options.

They can continue the attack.

They can retreat back to the village.

At this point we again need to assign Expected Utilities for both Marcus and the Indians.

If Marcus continues and the Indians retreat, he would continue to ride into the village. He would succeed in his orders. This the most favorable outcome and so we assign it +100 for Marcus.

But it's not so good for the warriors. They would lose the battle and their wives and children captured or killed. Very bad - a rating of -100.

Now if Marcus continues and the Indians continue, he will again have a mounted battle. This is not - oddly enough - the best for the cavalry - who fought their best by dismounting and forming skirmish lines. So for Marcus this is not a good situation but not the worse. We'll assign this as 0.

For the Indians, though, this is not that bad. They were trained to fight on horseback. It would be an activity for which they would receive honor as well. So for the warriors we'll rate this as +50.

What if Marcus dismounts and the Indians continue? Marcus and his men will fight in skirmish lines. The soldiers will be fighting as they have been trained to do. But they are also reduced in numbers since every 1 out of 4 men are assigned as horseholders. So this situations is - in principle - not the worst but not the best. So we'll rate this for Marcus as +25.

For the Indians, this is better than fighting a mounted foe. They can circle around the soldiers while they themselves are moving targets. In this situation this is the best for the warriors and so we'll rate this a +100.

And finally if Marcus dismounts and the Indians retreat, he will be waiting for George to show up. This gives him time to regroup and perhaps launch a new attack. We'll give this a rating of +50 for Marcus.

For the Indians, this is also fairly favorable. They will have time to return to the village and help their wives and families get away. But they will still have a sizable group of soldiers to contend with. For the Indians we'll rate this as +25.

So all of this makes up the table:

The game tree for this situation is (which opens in a new window to show how to eliminate the non-rational strategies):

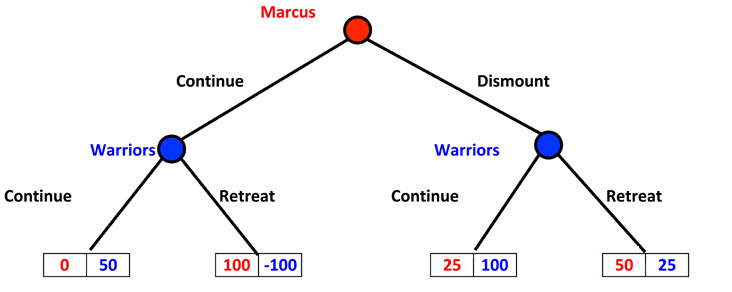
Game Tree: Marcus Skirmishes
(Click on image to open up the animated tree)

Notice now that whether you use the game tree - with the sequential moves - or the table - treating everything as simultaneous - it's the Indians who have the strictly dominant strategy: Continue (the Attack). That is because 50 > -100> and 100 > 25. Therefore the Indians will never retreat. So Marcus, knowing game theory, will then select "Dismount".

This is - again - exactly what happened.

Marcus and the Indians are continuing to act quite rational.

Certainly for now.

Marcus's Next Move

Marcus said it was a charge, sir!

At this point Marcus and his men have dismounted and formed a skirmish line. The Indians have continued their attack. There are - as always - new options.

Marcus can stand at his skirmish line and fight.

Or he can retreat across the river.

The options for the warriors are:

They can continue the attack.

They can retreat back to the village.

And as far as the "payoffs" - the "Expected Utilities" - we assign them as follows:

The best for Marcus is he stands and the Indians retreat. So we'll give Marcus +100 for this.

But this is not greatly favorable for the Indians. They get away back to the village so they can arrange the escape of the women and children. But they ultimately will be vulnerable to pursuit. So the Indians get a +25.

Marcus can stand and the Indians can continue their attack. Once more Marcus and his men are fighting as they are trained to do and there was also a stand of timber where Marcus could take his men for added protection. Still, the Indians will be at a bit of an advantage. So we assign Marcus a +50 and the Indians +75.

And if Marcus retreats and the Indians continue? At first glance this might not be that bad as Marcus is getting away. But actually it's the worst thing Marcus could do. You never simply ran from an attack of Indians who were exceptionally skilled in overtaking and killing a fleeing foe - an activity the Indians referred to as a "buffalo hunt". Marcus gets -100 and the Indians +100.

If both retreat? Well, Marcus comes off better, but he will not have succeeded in his orders. At best this is neutral so we give Marcus an Expected Utility of 0. The Indians, though, fare better and can return to the village to help evacuate the women and children. So they get a +50.

This can all be put in a table as:

The analysis here is straightforward as both Marcus and the Indians have a strictly dominant strategy. We see that the best strategy for Marcus is to stand because 50 > -100 and 100 > 25. And the Indians should continue since 75 > 25 and 100 > 50.

If you work through the game tree (again click on the image to see how to discard the non-rational strategies), we see the same thing.

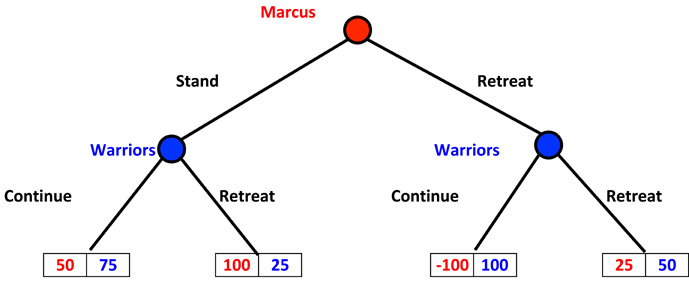
Marcus's "Charge
(Click on image to open the animated tree)

OK. but what really happened at the Little Bighorn?

In this case, Marcus did not chose the rational strategy. Instead, he retreated across the river. When asked if the men were demoralized by the "rout", Marcus replied, "That was a charge, sir!"

And the Indians?

Well, the Indians should have continued - that was, after all, the strictly dominant strategy. And if Marcus retreated, the Indians continuing would be the best possible outcome for them.

But the Indians didn't continue either. Instead, they also retreated and concentrated their efforts at another group of soldiers - at a place now called Custer Hill.

So What's the Problem?

OK. So why do some people trash game theory and say it fails the criteria to be a true science?

Remember, the modern definition of a science is one that can be tested. That is, the theory must make testable predictions in a clear cut an objective manner.

More explicitly a theory must be falsifiable. That is, there must be a test that will prove the theory false provided, of course, it is indeed false.

But note that game theory - at least in the simple examples here - doesn't have anything to test. It classifies actions as rational or irrational. But note these terms are definitions and more importantly, defintions that were constructed by the rules of game theory itself.

Such operational definitions are common in social sciences. One important example is IQ. Take a psychology class and the professor will point out that IQ - despite it's being thought of as measure of inborn or inherent intelligence - continues to resist a workable definition. So we define IQ simply as the score on an IQ test.

So in game theory the "rational" choice is the choice defined as rational by game theory. But we saw that in the examples above, "rational" is simply what remains after step wise elimination of the worst possible outcomes. But there are other definitions that will serve our purpose quite well, thank you.

It may be well worthwhile to take a risk of the worst possible outcome if there is a chance of a large benefit and the worst outcome is not particularly severe. A human being can quite legitimately call this a rational choice, but because it doesn't follow their definition, game theorists say it is irrational.

As far as being testable, game theory makes no claim that the rational actions is what people will do. People may very well choose the "irrational" strategy. A theory that doesn't produce anything to test is hardly a testable theory.

To iterate the point we've iterated, game theory is a computational method which was initially developed by analyzing games. Furthermore it does not make predictions but simply classifies actions as rational or irrational. It does not! not! not! say people will pick the rational choice.

So its no surprise in application to situations which are not exactly games and where you use it to predict behavior - like economics, war, or busienss - can fall flat. But the reader will be shocked! shocked! to learn that when used to analyze games - tic-tac-toe (that's "noughts and crosses" for the Brits), nim, rock-sissors-paper, and even chess - it works pretty darn well.

Marcus's Last Game

Marcus and Ella

After the Battle of the Little Bighorn, Marcus was often trashed by historians and even some of his fellow soldiers. Miffed at the increasingly bad publicity, in 1878 he asked for an inquiry - which was not a court-martial - and the board met in Chicago on January 13, 1879. After almost a month and much testimony, the court concluded that although Marcus had scarcely distinguished himself, nothing he did was improper or showed evidence of cowardice.

Well, that settles things, nicht wahr.

Well, nicht.

People who didn't like Marcus claimed - and still do - that the inquiry was a whitewash. With George dead, the Army already had their scapegoat. In fact, ex-President Hiram Grant had already issued his opinion that George Custer was solely responsible for the debacle. And who would contradict a presidential pronouncement?

But what is not well known is that the Reno Court of Inquiry was held after Marcus had been reinstated into the Army after another inquiry into his conduct. And this inquiry was a court-martial.

Right after the Little Bighorn, Alfred, Marcus and the rest returned to Fort Abraham Lincoln after spending nearly three months in the field. The officers decided to relax at the officers' club. There were generous libations and conversation, and soon Marcus found himself embroiled in an argument with another officer over the actions at the battle. Hard words passed and soon the two men were throwing rather ineffectual punches at each other. Eventually they were separated, but the matter was referred to the commanding officer - Colonel Samuel Sturgis. Samuel called the incident a "drunken debauch".

Now given the stresses and strains of the past months, it's understandable that there would be some hard feelings between soldiers so other than Colonel's Sturgis's rebuke, nothing was done. Unfortunately, Marcus also began annoying the pretty wife of a fellow officer, Captain James Bell who was away from the fort on an assignment. Mrs. Bell said that Marcus had run his hand along her arm and later placed his hands on her waist. Then after she understandably gave Marcus the cold shoulder by not inviting him to a Christmas party, he began spreading rumors that she was of poor character. He also denied her the privilege at the next church services to - with an unintended double entendre - to "play the organ".

Naturally when Captain Bell returned he was quite miffed, and he filed charges against Marcus. Colonel Sturgis tried to get Marcus to mediate a reconciliation with Mrs. Bell and her husband, but that effort failed. So a new set of charges regarding his conduct toward Mrs. Bell were added to the original list.

The charges of Mrs. Bell were quite serious and were listed as being "to the scandal and disgrace of the service." Such a description mandated dismissal if Marcus was found guilty. Well, he was found guilty but President Hayes reduced the sentence to suspension from rank and pay for two years.

In 1879 Marcus returned to active duty and appeared at the Court of Inquiry which cleared him of wrongdoing at the Little Bighorn. So all's well that ends well.

Weeeeelllllll, there's just one thing.

Marcus soon found himself in trouble again. And it was once more about rowdy behavior - and his conduct toward a lady. After playing billiards at a local emporium, he argued with a fellow officer over a bet, knocked some coins from the bartender's hands, and tossed a chair out of a window.

And yes, Marcus was once more scheduled for court martial. While waiting for the trial and technically under arrest, his movements at the fort were restricted. He was not even supposed to approach the house of Colonel Sturgis without prior permission.

And so ....

As evening came, Colonel Sturgis's 20 year-old daughter, Ella, was sitting in the parlor reading a book. As Marcus walked by, he saw Ella sitting there, looking pretty as a picture. At this point Marcus had two options.

He can continue on to his quarters or he can go peep at Ella through the window.

Likewise Ella has some choices.

She can say nothing or report Peeping Marcus to her father.

At this point we can assign Expected Utilities to the various outcomes.

The best thing for Marcus is to keep going by and for Ella not to say anything to her father. So we'll give this a +100 for Marcus. It's also the best thing for Ella since if Marcus didn't look in her window she shouldn't say anything. So this is +100 for Ella, too.

Now if Marcus peeks through the window and Ella reports the matter to her dad, this is very bad for Marcus. We'll give this a -100. It's also not the best for Ella as it will involve her in what we can call "unpleasantness". On the other hand she is telling the truth. So we'll give this situation a +50 for Ella.

Now if Marcus keeps going by and Ella tells her dad that Marcus looked in her window, this is very bad for Marcus, but not as bad as if he really had done it. After all, he might be able to prove his case - maybe some other officer saw him go on by. But it's still bad so we'll give this a -50 for Marcus. For Ella, this isn't good either. She not telling the truth to her dad and also involving herself in unpleasantness as if it really happened. We'll call this the worst case for Ella: -100.

If Marcus peeks through the window and Ella doesn't report the matter, this is pretty much neutral for both. Marcus doesn't get reported and Ella lets the matter drop. So we'll give them both 0 utility for this possibility.

Now the table for this incident is:

Now at this point we can make the game tree - again a clickable animation to show how to weed out the bad strategies - which looks like this:

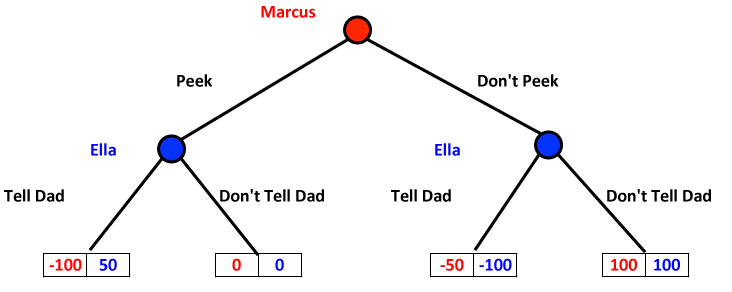
Marcus and Ella
(Click on image to open the animated tree)

For Ella, there is no dominant strategy (50 > 0, but -100 < 100). But for Marcus he really has only one rational choice. Since -50 > -100 and 100 > 0, Marcus's only option - the strictly dominant strategy - is not to peek. Which is not only rational, but makes sense.

And once Ella - who also knows game theory - knows Marcus will not peek, she decides she will not have to tell her dad.

Remember this is the most rational choice for both parties.

But which actually happened?

Well, Marcus did peek. He not only peeked but rapped on the window.

Ella completely freaked out and was so seriously "affrighted" that she almost suffered from "St. Vitus Dance". But she had the presence of mind to look at the game theory tree. If Marcus peeks, she sees the Expected Utility of 50 (Tell Dad) trumps 0 (Don't Tell Dad). So she knows she should tell her dad.

Which is what she did.

With one more very serious charge against him, Marcus was summoned to the court martial. Again due to the technical reading of the finding, the only option for the court was dismissal from the service.

The officers of the court, though, recommended that the penalty be reduced to suspension from rank and pay for one year. But now they hit a snag when the report was referred for final review to Major Henry Goodfellow of the Bureau of Military Justice.

Henry pointed out that Marcus had a recent conviction for charges of similar severity. He had received a reduced penalty then as well. Were they to continue to grant leniency to an officer of over twenty years service in an army that had no hesitation in dismissing wayward cadets from West Point? Although Henry did not insist Reno be dismissed, his review persuaded Secretary of War Alexander Ramsey that enough was enough. Alexander said there should be no clemency. President Hayes agreed, and Marcus was out of the army for good.

Marcus spent the rest of his life trying to get reinstated. Everything he tried, including Congressional action, failed. Then on March 30, 1889 he died of pneumonia arising from an operation to remove a cancerous growth on his tongue.

Marcus, though, still had his defenders who continued to work for his vindication. But it took a while. It wasn't until 1967 that a military board agreed to review his court martial record. After the hearing they decided the sentence had indeed been too harsh. So Marcus was given a belated honorable discharge and was reburied in the military cemetery at the Little Bighorn.

Rational Marcus

So what caused Marcus's problems?

Well, we can see that whatever the definition of rational and irrational, Marcus had trouble when he opted to take the least rational option - at least as defined by game theory - out of those available. And whether the decision had to do with fighting a battle, socializing with his fellow officers, or paying tribute to feminine beauty, when he made the irrational choice, it was a whopper.

But what about George Armstrong Custer? Did he make the rational choices?

Well, that, as they say, is another story.

References

A Terrible Glory: Custer and the Little Bighorn - The Last Great Battle of the American West, James Donovan, Little Brown and Company (2008).

Cavalier in Buckskin: George Armstrong Custer and the Western Military Frontier, Robert M. Utley, University of Oklahoma Press, (1988).

Lakota Noon, Gregory F. Michno, (Mountain Press Publishing, 1997).

Reno Court of Inquiry: Proceedings of a Court of Inquiry in the Case of Major Marcus A. Reno. Concerning His Conduct at the Battle of the Little Bighorn River on June 25-26, 1876, Ron Nichols , Custer Battlefield Historical and Museum Association, (1996).

In Custer's Shadow: Major Marcus Reno Ronald Nichols, Old Army Press (1999), University of Oklahoma Press (2000).

Game Theory 101: The Complete Textbook, William Spaniel, CreateSpace, 2011

The Prisoners' Dilemma, William Poundstone, Doubleday, 1992.

"A Nobel Letdown in Economics", Michael Mandel, Bloomberg Business, October 10, 2005

A Beautiful Mind, Sylvia Nasar, Simon and Schuster, 1998.

"John Nash", MacTudor History of Mathematics, http://www-history.mcs.st-and.ac.uk/Mathematicians/Nash.html.

"Does Game Theory Work?", Michael Wooldridge, IEEE Intelligent Systems, November/December 2012.

CooperToons Merry History

CooperToons Department of Education

CooperToons Home Page